Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT ENGLISH-NUCLEI-Exercise
- Consider the following nuclear fission reaction .(88)Ra^(226) to ....
Text Solution
|
- The radionuclide .6C^(11) decays according to .6C^(11)to .5B^(11) +e^(...
Text Solution
|
- The nucleus .^(23)Ne deacays by beta-emission into the nucleus .^(23)...
Text Solution
|
- The Q value of a nuclear reaction A+b=C+d is defined by Q=[mA+mb-mC-...
Text Solution
|
- Suppose, we think of fission of a .26Fe^(56) nucleus into two equal fr...
Text Solution
|
- The fission properties of .84Pu^(239) are very similar to those of .92...
Text Solution
|
- A 1000 MW fission reactor consumes half of its fuel in 5.00yr. How muc...
Text Solution
|
- How long can an electric lamp of 100W be kept glowing by fusion of 2.0...
Text Solution
|
- Calculate the height of potential barrier for a head on collision of t...
Text Solution
|
- from the relation R=R0A^(1//3), where R0 is a constant and A is the ma...
Text Solution
|
- for the beta^(+) (positron) emission from a nucleus, there is another ...
Text Solution
|
- In a periodic table, the average atomic mass of magnesium is given as ...
Text Solution
|
- The neutron separation energy is defined to be the energy required to ...
Text Solution
|
- A source contains two phosphorus radionuclides .(15)P^(35) (T(1//2)=14...
Text Solution
|
- Under certain circumstances, a nucleus can decay by emitting a particl...
Text Solution
|
- Consider the fission .(92)U^(238) by fast neutrons. In one fission eve...
Text Solution
|
- Consider the so called D-T reaction (deuterium-tritium fusion) .1H^2+....
Text Solution
|
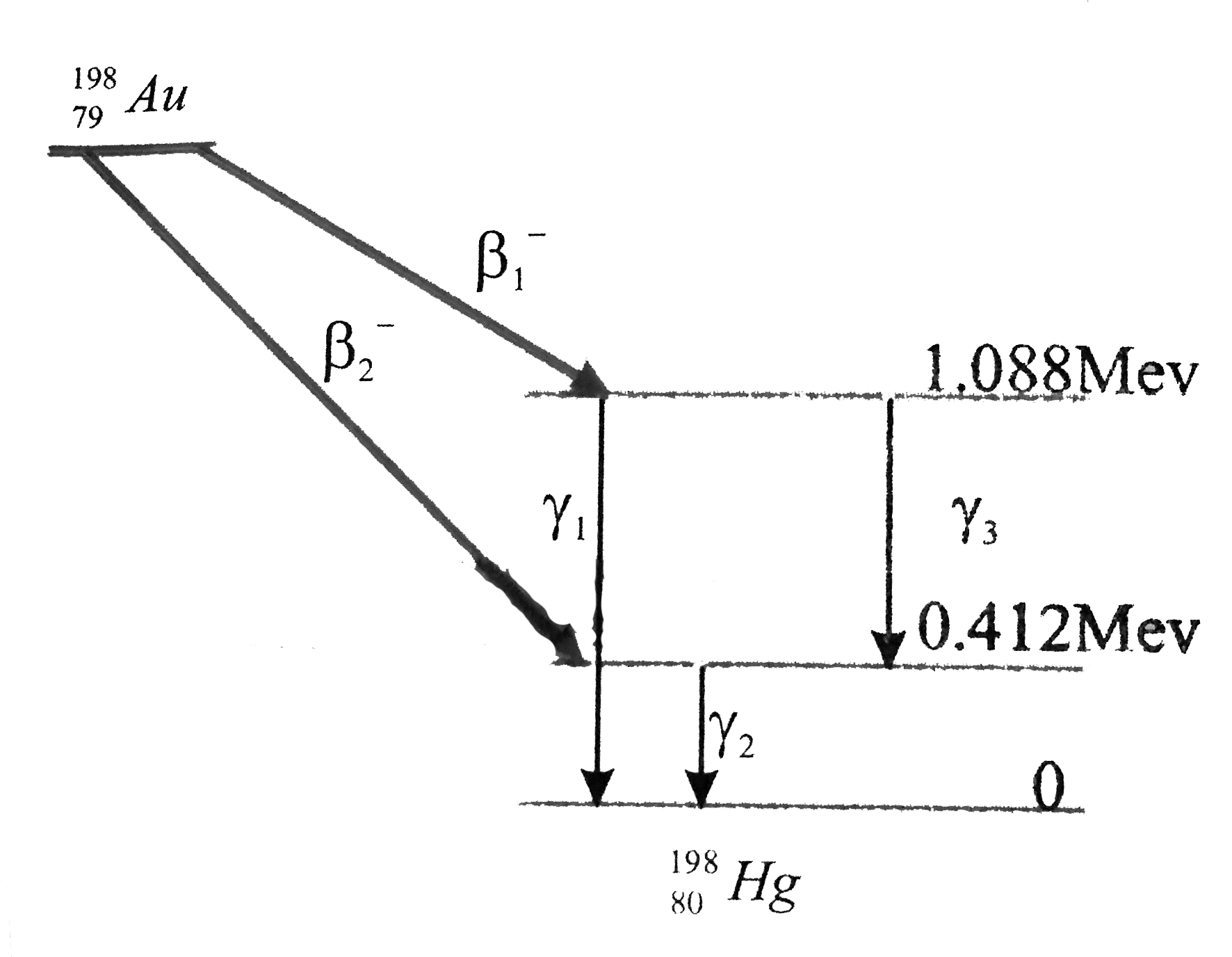
- Obtain the maximum kinetic energy of beta-particles, and the radiation...
Text Solution
|
- Calculate and compare the energy released by (a) fusion of 1.0kg of hy...
Text Solution
|
- Suppose India has a target of producing by 2020 AD, 200,000 MW of elec...
Text Solution
|