Text Solution
Verified by Experts
Topper's Solved these Questions
ELECTROSTATIC POTENTIAL AND CAPACITANCE
U-LIKE SERIES|Exercise LONG ANSWER QUESTIONS-I|64 VideosELECTROSTATIC POTENTIAL AND CAPACITANCE
U-LIKE SERIES|Exercise LONG ANSWER QUESTIONS-II|13 VideosELECTROSTATIC POTENTIAL AND CAPACITANCE
U-LIKE SERIES|Exercise VERY SHORT ANSWER QUESTIONS|40 VideosELECTROMAGNETICE INDUCTION
U-LIKE SERIES|Exercise Self Assessment Test Section -D|1 VideosEXAMINATION PAPER 2020 (SOLVED)
U-LIKE SERIES|Exercise SECTION D|6 Videos
Similar Questions
Explore conceptually related problems
U-LIKE SERIES-ELECTROSTATIC POTENTIAL AND CAPACITANCE -SHORT ANSWER QUESTIONS
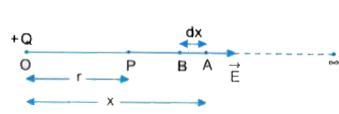
- Find an expression for the potential at a point due to a point charge ...
Text Solution
|
- How does electric potential vary from point to point due to a thin cha...
Text Solution
|
- Two spherical conductors of radii R, and R2 (R2 > Ri) are charged. If ...
Text Solution
|
- Draw a plot showing the variation of (i) electric field E, and (ii) e...
Text Solution
|
- Derive an expression for the electric potential at any point along the...
Text Solution
|
- Deduce an expression for the electric potential due to an electric dip...
Text Solution
|
- Show mathematically that the potential at a point on the equatorial li...
Text Solution
|
- Derive an expression for the work done in rotating an electric dipole ...
Text Solution
|
- A dipole is present in an electrostatic field of magnitude 10^6 NC^(-1...
Text Solution
|
- Calculate the amount of work done in turing an electric dipole of dipo...
Text Solution
|
- The electric field and electric potential at any point due to a point ...
Text Solution
|
- Calculate the electric potetial at the surface of a gold nucles. Given...
Text Solution
|
- The following data was obtained for the dependence of the magnitude of...
Text Solution
|
- A test charge 'q' is moved without acceleration from A to C along the ...
Text Solution
|
- An electric dipole is held in a uniform electric field. Show that th...
Text Solution
|
- An electric dipole is held in a uniform electric field. The dipole i...
Text Solution
|
- What is an equipotential surface ? Show that the electric field at a p...
Text Solution
|
- State main characteristics of an equipotential surface.
Text Solution
|
- Can two equipotential surfaces intersect each other? Give reasons.
Text Solution
|
- Two charges - q and + q are located at points A(0, 0, -a) and B(0, 0, ...
Text Solution
|