Text Solution
Verified by Experts
Topper's Solved these Questions
TRIANGLES
RS AGGARWAL|Exercise Exercise 8|13 VideosTRIANGLES
RS AGGARWAL|Exercise EXERCISE|16 VideosTRIANGLES
RS AGGARWAL|Exercise MULTIPLE-CHOICE QUESTIONS (MCQ)|10 VideosQUADRILATERALS
RS AGGARWAL|Exercise Matching of Columns:|2 VideosVOLUME AND SURFACE AREA OF SOLIDS
RS AGGARWAL|Exercise Multiple Choice Questions (Mcq)|73 Videos
Similar Questions
Explore conceptually related problems
RS AGGARWAL-TRIANGLES-EXAMPLE
- In a DeltaABC the sides AB and AC are produced to points D and E respe...
Text Solution
|
- In the given figure, the side BC of DeltaABC has been produced to a po...
Text Solution
|
- In a DeltaABC,angleBgtangleC."If "ADbotBCandAE is the bisector of angl...
Text Solution
|
- A DeltaABC is right angled at A and L is a point on BC such that ALbot...
Text Solution
|
- In the given figure, prove that x=alpha+beta+gamma.
Text Solution
|
- The side BC of DeltaABC is produced ot D. The bisector of angleA meets...
Text Solution
|
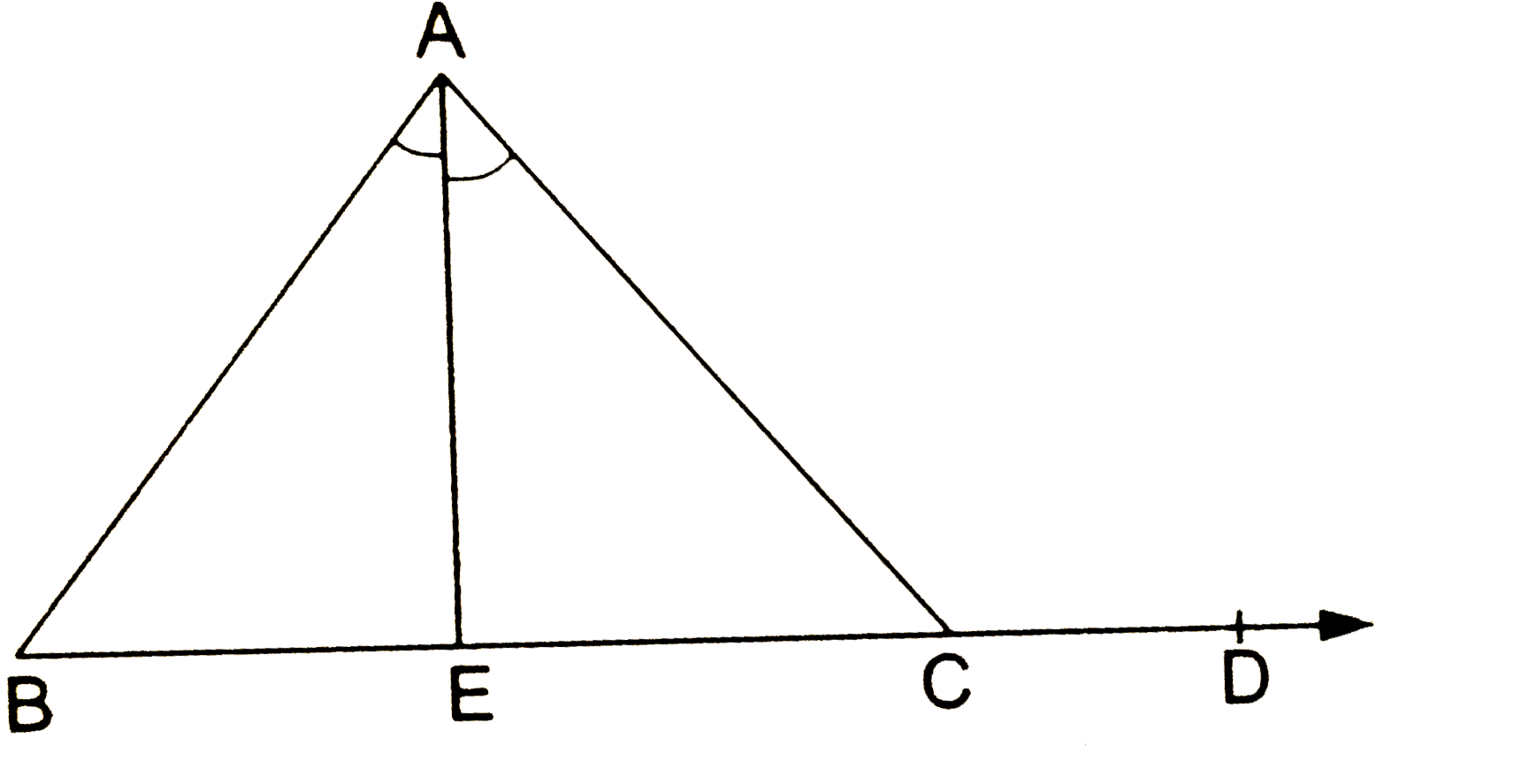
- In the given figure, side BC of DeltaABC is produced to form ray BD an...
Text Solution
|
- In DeltaABC it is given that angleA=70^(@),angleB=52^(@),BOandCO are t...
Text Solution
|
- In the given figure, PQbotPS,PQ||SR,angleSQR=28^(@)andangleQRT=70^(@)....
Text Solution
|
- In the given figure, lines AB and CD intersect at a point P such that ...
Text Solution
|