Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
RS AGGARWAL-AREAS OF PARALLELOGRAMS AND TRIANGLES -ASSERTION & REASON TYPE
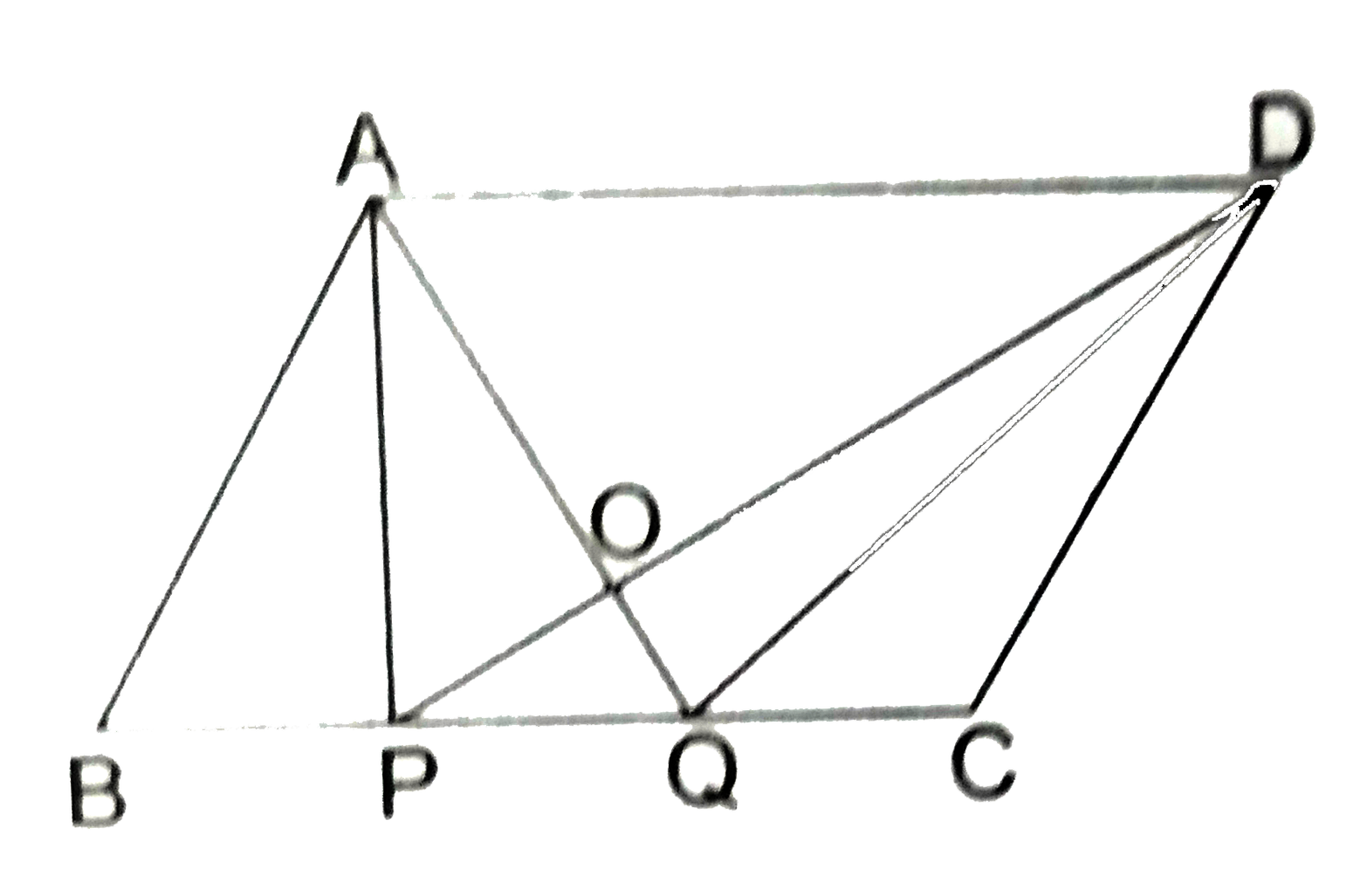
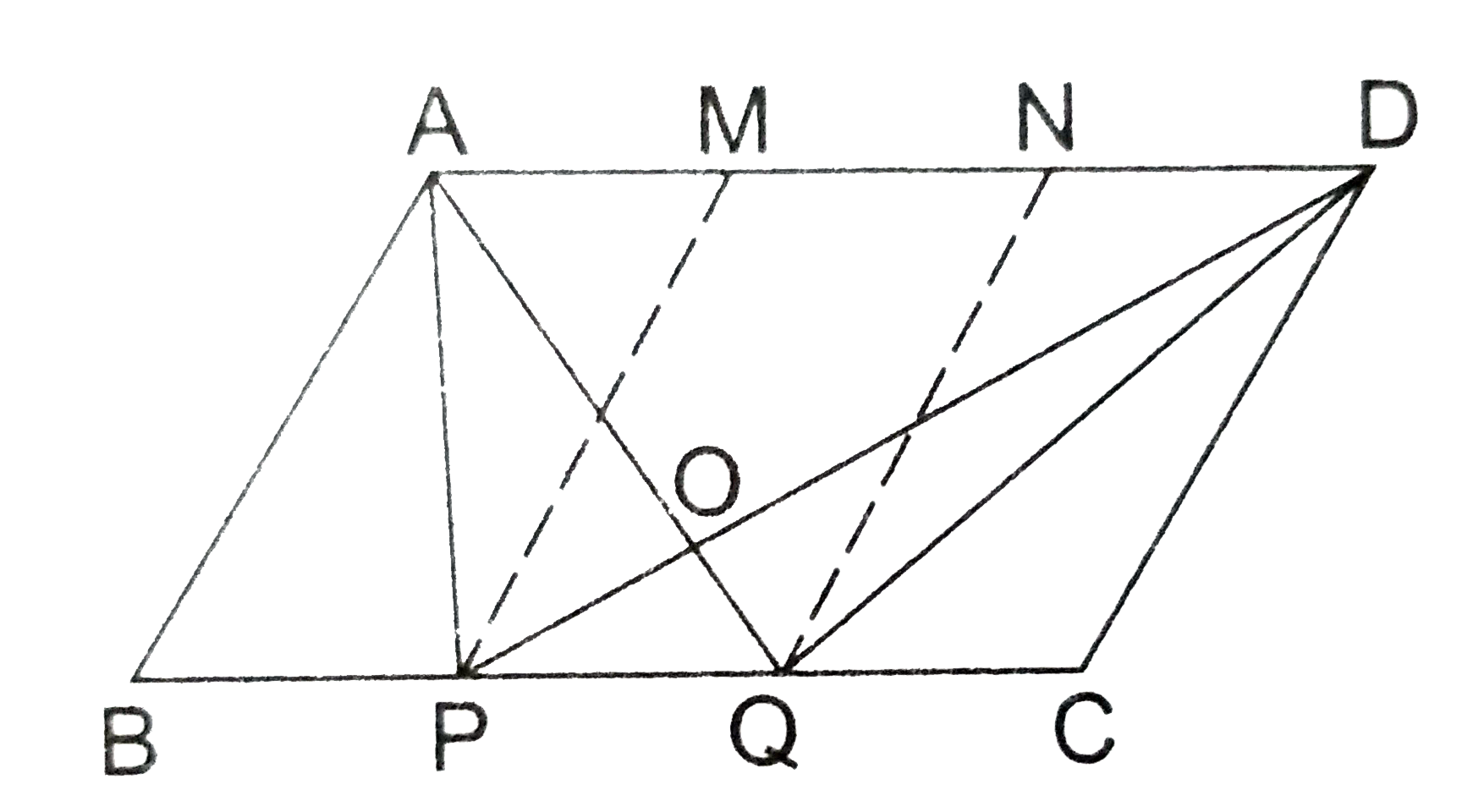
- In the adjoining figure, ABCD is a parallelogram. Points P and Q on BC...
Text Solution
|
- Assertion (A) : In a trapezium ABCD, we have AB ||DC and the diagonals...
Text Solution
|
- Assertion (A) : If ABCD is a rhombus whose one angle is 60^(@) then th...
Text Solution
|
- Asserion (A) : The diagonals of a ||gm divide it into four triangle of...
Text Solution
|
- Assertion (A) : The area of a trapezium whose parallel sides measure 2...
Text Solution
|
- Assertion (A) : In the given figlure, ABCD is a ||gm in which DEbotAD ...
Text Solution
|