In the adjoining figure, ABC and BDE are two equilateral triangle such that D is the midpoint of BC. If AE intersects BC at F, show that
`(i) ar(triangleBDE)= (1)/(4)ar(triangleABC)`
`(ii) ar(triangleBDE)=(1)/(2)ar(triangleBAE)`
`(iii) ar(triangleABC)=2ar(triangleBEC)`
`(iv) ar(triangleBFE)=ar(triangleAFD)`
`(v)ar(triangleBFE)=2ar(triangleFED)`
`(vi) ar(triangleFED)=(1)/(8)ar(triangleAFC)`.

Explanation

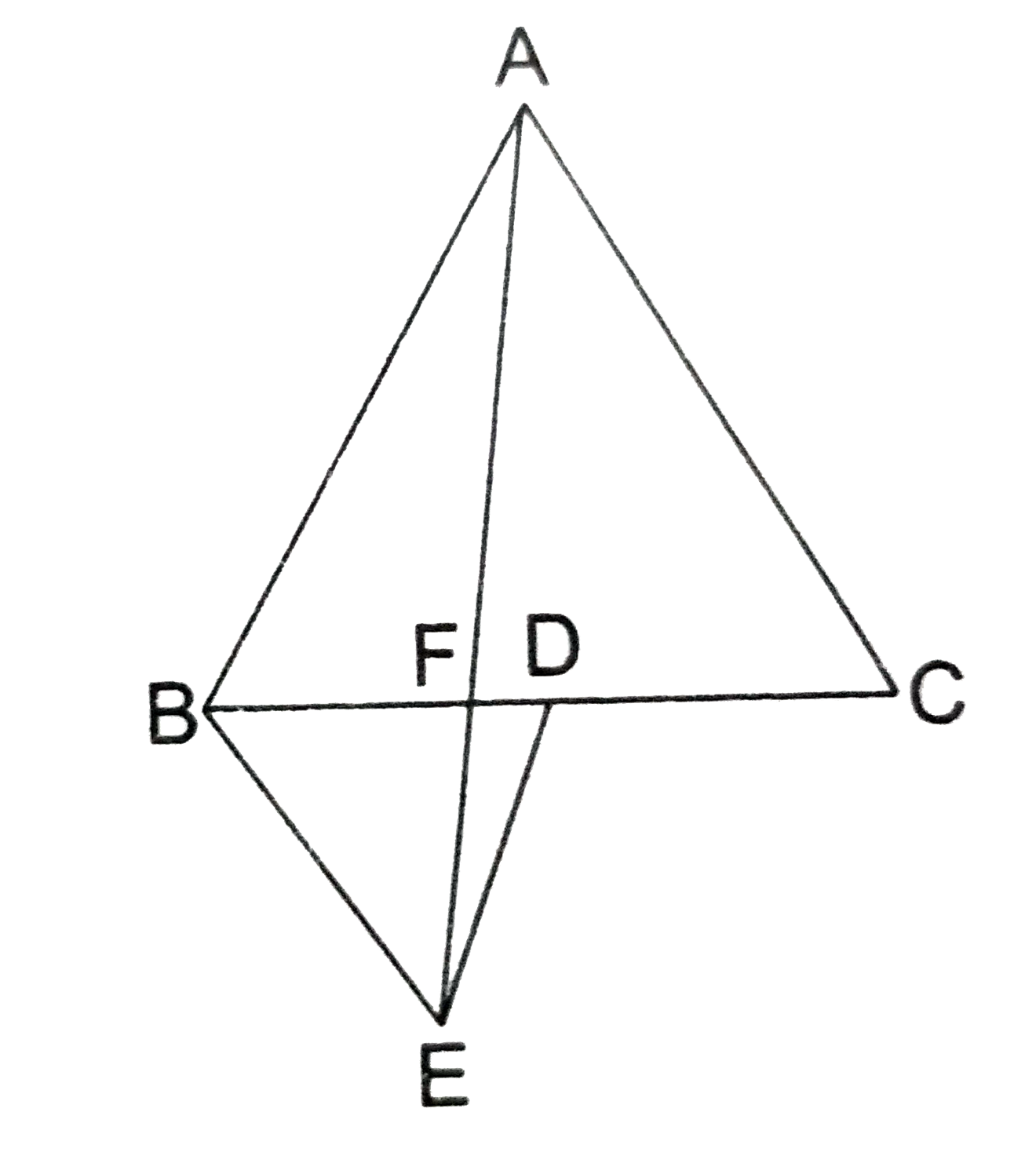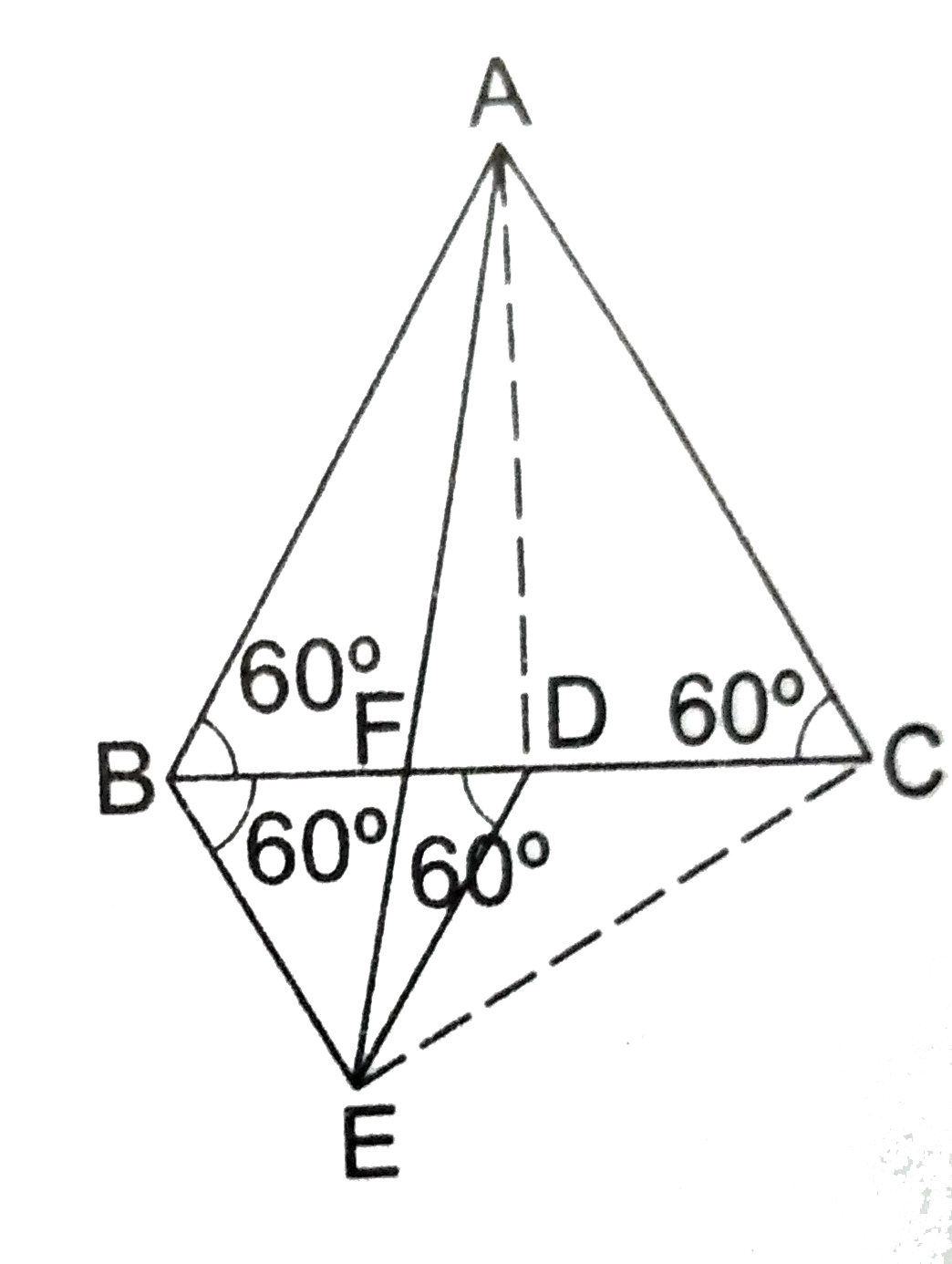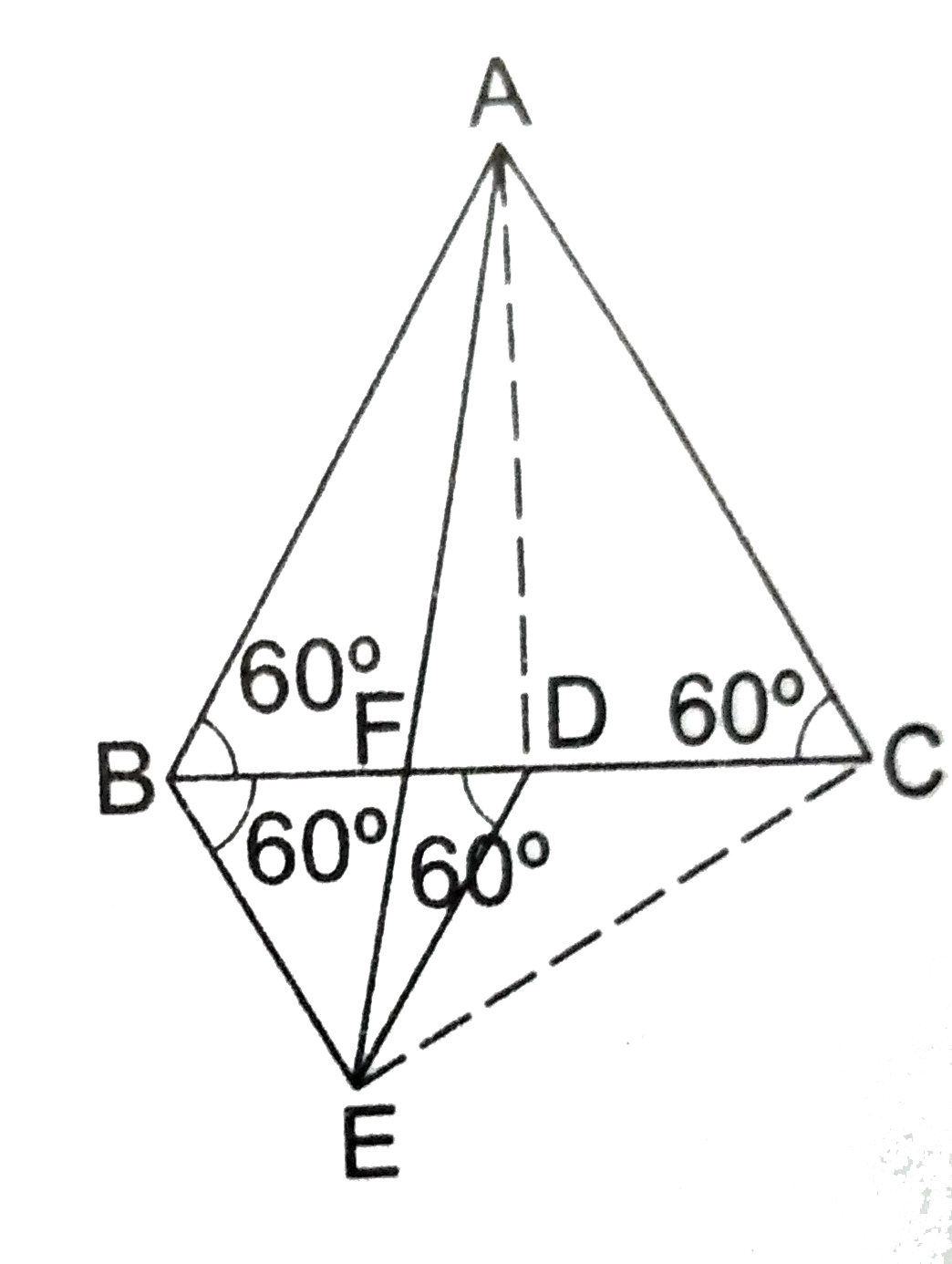
Join AD and EC.
We have `angleABC = angleDBE = 60^(@) rArr "DE||AB"`
(alt. interior `angle`)
and `angleACB =angleDBE = 60^(@) rArr "BE||AC"`
[`therefore triangleABC and triangleBDE " are eq." triangle`].
Now, let each side of `triangleBDE=a`.
Then, `ar(triangleBDE)=(sqrt3)/(4)a^(2)." "...(i)`
Each side of `triangle` ABC = 2a " " [`therefore BC = 2BD].`
`therefore ar(triangleABC)=(sqrt3)/(4)(2a)^(2)=4((sqrt3)/(4)a^(2))." "...(ii)`
From (i) and (ii), we get
`ar(triangleBDE)=(1)/(4)ar(triangleABC)." "...(iii)`
Now, AD is a median of `triangle ABC`
`rArr ar(triangleABD)=(1)/(2)ar(triangleABC)." "...(iv)`
But, `ar(triangleBAE)=ar(triangleABD)" "...(v)`
[`therefore` same base AB and same parallels AB and DE].
From (iv) and (v), we get
`ar(triangleBAE)=(1)/(2)ar(triangleABC)." "...(vi)`
From (iii) and (vi), we get
`ar(triangleBDE)=(1)/(2)ar(triangleBAE)." "...(vii)`
Now, `ar(triangleBDE)=(1)/(2)ar(triangleBEC)" "...(viii)`
`[therefore " ED is a median of " triangle BEC ]`
From (iii) and (viii), we get
`ar(trianglABC)=2ar(triangleBEC)" ...(ix)`
Now, `ar(triangleAED)=ar(triangleBDE)`
[`therefore` same base DE and parallels AB and DE]
`rArr ar(triangleAED)-ar(triangleFED)=ar(triangleBDE)-ar(triangleFED)`
`rArr ar(triangleAFD)=ar(triangleBFE)." "...(x)`
Now, height of `triangleAFD=" height of "triangleABC = H=(sqrt3)/(2)(2a)=sqrt3a`
and height of `triangle FED = " height of " triangleBDE = h =(sqrt3)/(2)(a)=(sqrt3)/(2)=(H)/(2)`.
`therefore ar(triangle AFD) = (1)/(2)xxFDxxH and ar(triangleFED)=(1)/(2)xxFDxx(H)/(2)`
` rArr ar(triangleAFD)=2ar(triangleFED)" "...(xi)`
`rArr (triangeBFE)=2ar(triangleFED)" "...(xii)` [using (x)].
Now, `ar(triangleAFC)=ar(triangleAFD)+ar(triangleADC)`
`=2ar(triangleFED)+(1)/(2){ar(triangleABC)}" "["using (xi)"]`
`=2ar(triangleFEd)+(1)/(2){4ar(triangleBDE)}` [using (iii)]
=`2ar(triangleFED)+2{ar(triangleBFE)+ar(triangleFED)}`
`=2ar(triangleFED)+2{ar(triangleFED)+ar(triangleFED)}`
[using (xii)]
`=8ar(triangleFED)`
`rArr ar(triangleFED)=(1)/(8)ar(triangleAFC)`.