Home
Class 12
CHEMISTRY
The number of octahedral voids in a unit...

The number of octahedral voids in a unit cell of cubic close packed structure is 

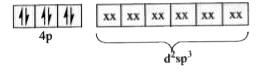
Text Solution

Verified by Experts

The correct Answer is:
4
`[Fe(CN)_(6)]^(4-)` (after rearrangement)
Promotional Banner

Topper's Solved these Questions

  • CO-ORDINATION COMPOUNDS

    AAKASH SERIES|Exercise PRACTICE SHEET - 4 ( Single or more than one option questions C.E.T., Stability, Applications:|16 Videos

  • CO-ORDINATION COMPOUNDS

    AAKASH SERIES|Exercise PRACTICE SHEET - 4 ( Linked Comprehension type questions) Passage-I|3 Videos

  • CO-ORDINATION COMPOUNDS

    AAKASH SERIES|Exercise PRACTICE SHEET - 3 ( Match the following questions)|2 Videos

  • CHEMISTRY IN EVERYDAY LIFE

    AAKASH SERIES|Exercise PRACTICE SHEET - 2 (PRACTICE SHEET -2 (INTEGER ANSWER TYPE QUESTIONS))|7 Videos

  • COMPLEX COMPOUNDS

    AAKASH SERIES|Exercise PRACTICE EXERCISE|45 Videos

Similar Questions

Explore conceptually related problems

The number of atoms in a single unit cell of cubic close packed sphere is ---------

The number of tetrahedral voids in the unit cell of a face-centred cubic lattice of similar atoms is

The number of tetrahedral and octahedral voids in CCP unit cell are respectively

The number of carbon atoms per unit cell of diamond unit cell is

(i) What is meant by the term 'coordination number'? (ii) What is the coordination number of atoms: (a) in a cubic close-packed structure? (b) in a body-centred cubic structure?

The number of atoms in a face centred cubic unit cell is:

If the radius of the octahedral void is r and radius of the atoms in close packing is R , derive relation between r and R .

Aluminium crystallizes in a cubic close packed structure . Its metallic radius is 125 pm . What is the length of the side of the unit cell .

Aluminium crystallizes in a cubic close packed structure . Its metallic radius is 125 pm . How many unit cells are there in 1.00 cm^(3) of aluminium.

If R is the radius of the octahedral void and r is the radius of the atom in close packing, then r/R is equal to