Text Solution
Verified by Experts
RS AGGARWAL-AREA OF BOUNDED REGIONS -Exercise 17
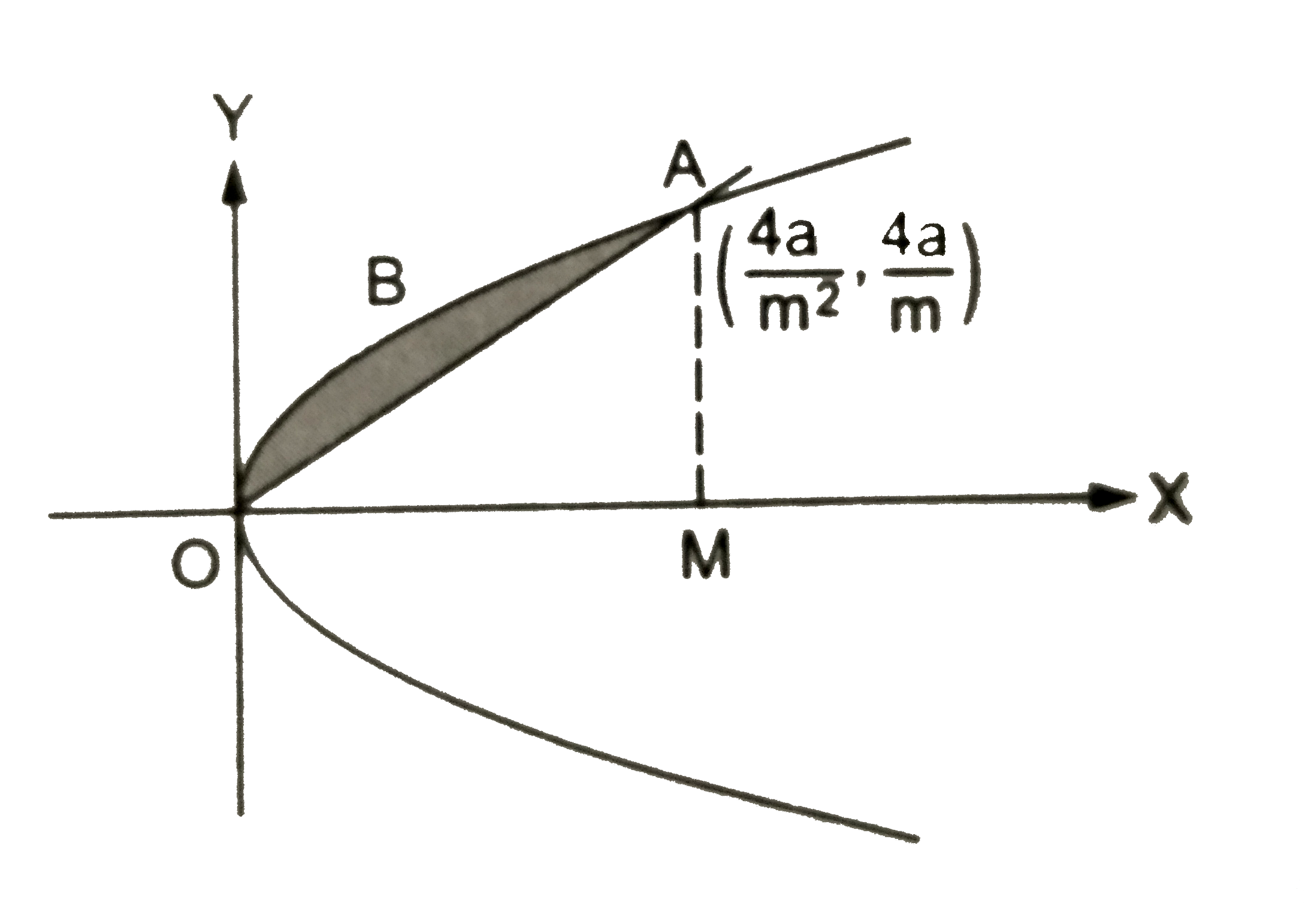
- Find the area enclosed between the parabola y^2=4a x and the line y =...
Text Solution
|
- Find the area of the region bounded by the curve y = x^2 , the x-axis,...
Text Solution
|
- Find the area of the region bounded by the parabola y^2 = 4x, the x-ax...
Text Solution
|
- Find the area under the curve y=sqrt(6x+4)(above the x-axis) from x=0 ...
Text Solution
|
- Determine the area enclosed by the curve y=x^3 , and the lines y=0,x=2...
Text Solution
|
- Determine the area under the curve y=sqrt(a^2-x^2) included between th...
Text Solution
|
- Using integration, find the area of the region bounded by the line 2y ...
Text Solution
|
- Find the area of the region bounded by the curve y^2=4x and the line ...
Text Solution
|
- Evaluate the area bounded by the ellipse (x^2)/(4)+(y^2)/(9)=1 above...
Text Solution
|
- Using integration, find the area of the region bounded by the lines Y ...
Text Solution
|
- Find the area bounded by the curve y=(4-x^2) the y-axis and the lines ...
Text Solution
|
- Using integration, find the area of the region bounded by the triangle...
Text Solution
|
- Using integration, find the area of the region bounded by the lines...
Text Solution
|
- Using intergration find the are of the region bounded between the lin...
Text Solution
|
- Using integration, find the area of the region bounded by the line y-1...
Text Solution
|
- Sketch the region lying in the first quadrant and bounded by y = 4x^2 ...
Text Solution
|
- Sketch the region lying in the first quadrant and bounded by y=9x^2...
Text Solution
|
- Find the area of the region enclosed between the two circles x^2 + y^2...
Text Solution
|
- Sketch the region common to the circle x^2 +y^2=16 and the parabola x...
Text Solution
|
- Sketch the region common to the cirvle x^2+y^2=25 and the parabola y^...
Text Solution
|
- Draw a rough sketch of the region {(x,y): y^2 le 3x,3x^2 + 3y^2 le16 }...
Text Solution
|