Home
Class 11
PHYSICS
A mass of 4 kg rests on a horizontal pla...

A mass of 4 kg rests on a horizontal plane. The plane is gradually inclined until at an angle `0 = 15^(@)` with the horizontal, the mass just begins to slide. What is the coefficient of static friction between the block and the surface

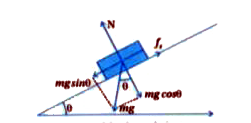
Text Solution

Verified by Experts


Force acting on block and their component are shown in figure
When `theta ` increases tan `theta` will also increase hence magnitude of `f_(s) ` will increase upto certain limit Let for `theta = theta_(max)` frictional force become maximum `f_(s) _(max)` from equatin (3)
`tan theta _(max)`
`tan 15^(@) =mu_(s)`
`mu_(s) = tan 15^(@) = 0.2679`
`mu_(s) = 0.27`
Promotional Banner

Topper's Solved these Questions

  • LAW OF MOTION

    KUMAR PRAKASHAN|Exercise SECTION -B (NUMERICAL FROM TEXTUAL EXERCISE)|23 Videos

  • LAW OF MOTION

    KUMAR PRAKASHAN|Exercise SECTION -B (ADDITIONAL EXERCISE )|17 Videos

  • LAW OF MOTION

    KUMAR PRAKASHAN|Exercise SECTION-A(QUESTION PAPER)|39 Videos

  • GRAVITATION

    KUMAR PRAKASHAN|Exercise QUESTIONS PAPER Section - D|1 Videos

  • MACHANICAL PROPERTIES OF SOLIDS

    KUMAR PRAKASHAN|Exercise QUESTION PAPER|11 Videos

Similar Questions

Explore conceptually related problems

A block of mass m lying on a rough horizontal plane is acted upon by a horizontal force P and another force Q inclined at an angle theta to the vertical. The minimum value of coefficient of friction of friction between the block and the surface for which the block will remain in equilibrium is

A block lying on a rough horizontal surfaces as show in figure . Its mass is M and it is dispalced through a distance d by a force vec(F ) acting at an angle theta with horizontal . If mu is the coefficient of friction between a block and the surface and mass of block is M . then work done is ...........

A rocket is fired vertically from the earth with an acceleration of 2g, where g is the gravitational acceleration. On an inclined plane inside the tocket, making an angle theta with the horizontal, a point object of mass m is kept, the minimum coefficient of friction mu_(min) between the mass and the inclined suface such that the mass does not move is:

A projectile si thrown with velocity of 50m//s towards an inclined plane from ground such that is strikes the inclined plane perpendiclularly. The angle of projection of the projectile is 53^(@) with the horizontal and the inclined plane is inclined at an angle of 45^(@) to the horizontal. (a) Find the time of flight. (b) Find the distance between the point of projection and the foot of inclined plane.

A plank w ith a box on it atone end is gradually raised about the other end . As the ang le of in clin ation with the horizontal reaches 30^(@) , the box starts to slip and slides 4.0 m down the plan k in 4.0s. The coefficients of static and k inetic friction between the box and the plank will be, respectively:

A body of mass 5xx10^(-3) kg is launched upon a rough inclined plane making an angle of 30^(@) with the horizontal. Obtain the coefficient of friction between the body and the plane if the time of ascent is half of the time of descent.

A block of mass m1 = 1 kg another mass m2 = 2 kg, are placed together (see figure) on an inclined plane with angle of inclination theta . Various values of theta are given in List I. The coefficient of friction between the block m_(1) and the plane is always zero. The coefficient of static and dynamic friction between the block m_(2) and the plane are equal to mu = 0.3 . In List II expressions for the friction on block m_(2) are given. Match the correct expression of the friction in List II with the angles given in List I, and choose the correct option. The acceleration due to gravity is denoted by g [Useful information : tan (5.5^(@)) ~~ 0.1, tan (11.5^(@)) ~~ 0.2 , tan (16.5^(@))~~ 0.3 ].

A block rests on a rough inclined plane making an angle of 30° with the horizontal. The coefficient of static friction between the block and the plane is 0.8. If the frictional force on the block is 10 N, the mass of the block ((in kg) is .......... (Take g = 10 m//s^(2) )

Two blocks of masses m_(1)=1 kg and m_(2)=2 kg are connected by a string and side down a plane inclined at an angle theta=45^(@) with the horizontal. The coefficient of sliding friction between m_(1) and plane is mu_(1)=0.4, and that between m_(2) and plane is mu_(2)=0.2. Calculate the common acceleration of the two blocks and the tension in the string.

force F = 100 N is applied horizontally on a block of mass 4 kg. Which is in contact with a wall. Such that it does not fall. The coefficient of friction between the block and the wall is