Let M be the set of students who passed in Mathematics, E be the set of students who passed in English and S be the set of students who passed in Science.
Then, `n(u) = 100`,
`n(E) = 15, n (M) = 12, n (S) = 8, n (E nn M) = 6, n(M nn S) = 7`,
`n(EnnS) = 4`, and `n(E nn M nn S) = 4`.
`:. n(E) = 15`
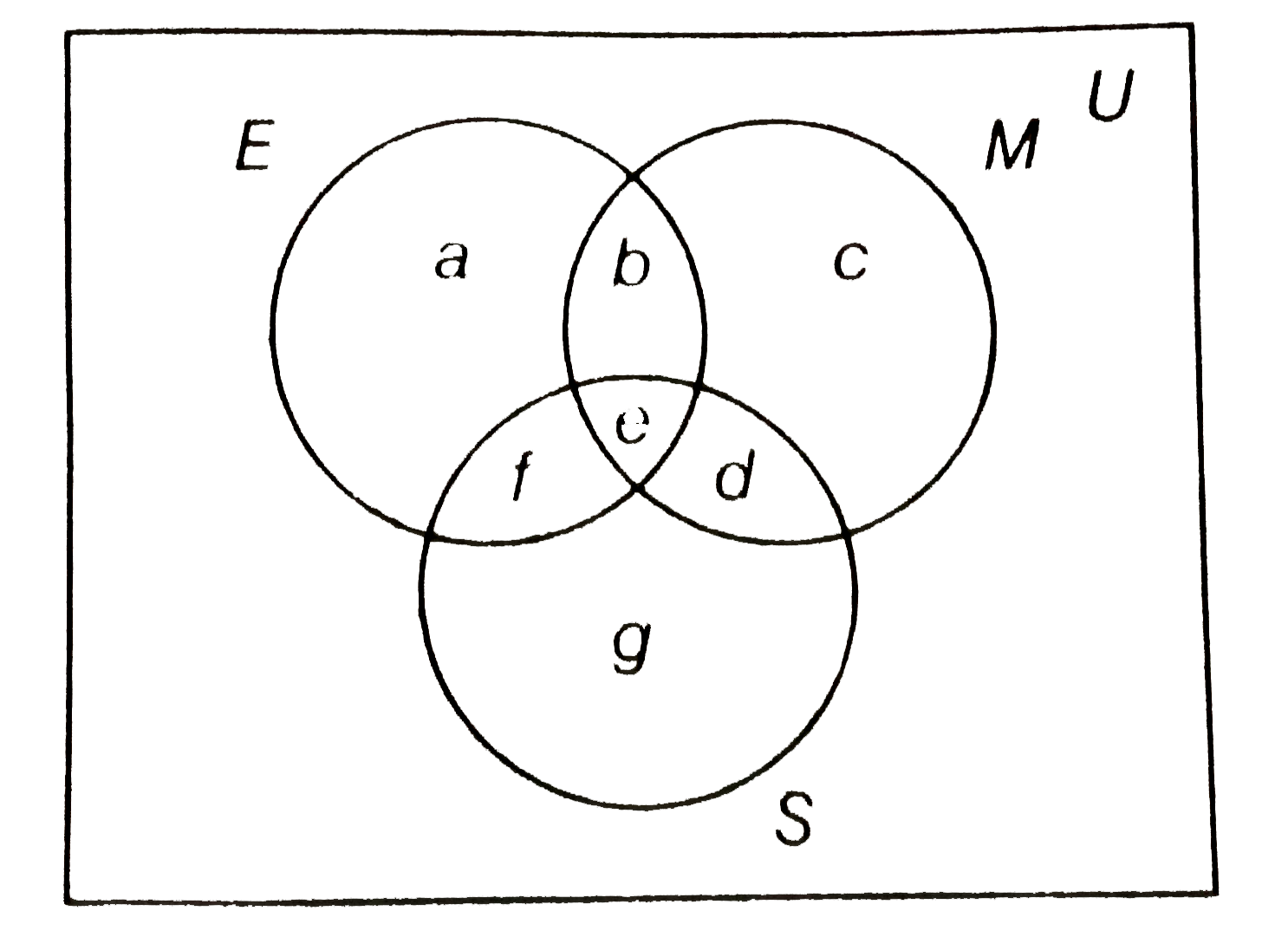
`rArr a + b + e + f = 15 "....."(i)`
and `n(M) = 12`
`rArr b + c + e + d = 12 "....."(ii)`
Also, `n(S) = 8`
`rArr d + e + f + g = 8 "......."(iii)`
`n(E nn M) = 6`
`rArr b + e = 6 "......."(iv)`
`n(M nn S) = 7`
`rArr e + d = 7"......"(v)`
`n(E nn S) = 4`
`rArr e + f = 4"......."(vi)`
`n(E nn M nn S) = 4`
`rArr e = 4 "......."(vii)`
From Eqs. (vi) and (vii), `f = 0`
From Eqs. (v) and (vii). `d = 3`
From Eqs. (iv) and (vii). `b = 2`
On substiuting the values of d, e and f in Eq. (iii), we get
`3 + 4 + 0 + g = 8`
`rArr g = 1`
On substituting the value of b, e and d in Eq. (ii) we, get
` 2 + c + 4 + 3 = 12`
`rArr c = 3`
On substituting b, e, and f in Eq. (i), we get
`a + 2 + 4+ 0 = 15`
` rArr a = 9`
(i) Number of students who passed in English and Mathematics but not in Science
`= b = 2`
(ii) Number of students who passed in Mathematics and Science but not in English
`= d = 3`
(iii) Number of students who passed in Mathematics only `= c = 3`
(iv) Number of students who passed in more than one subject
`= b +e + d + f`
` = 2 + 4 + 3 + 0 =9`
Alternate Method
Let E denote the set of student who passed in English. M denotes the set of students who passed in Mathematics. S denotes the set of students who passed in Science.
Now, `n(U) = 100, n(E) = 15, n(m) = 12, n(S) = 8`,
`n(E nn M) = 6, n(M nn S) = 7`,
`n(E nn S) = 4, n(E nn M nn S) = 4`
(i) Number of students passed in English and Mathematics but not in Science
i.e., `n(E nn M nn S') = n(E nn M) - n(E nn M nn S) , [:' A nn B' = A - (A nn B)]`
`= 6 - 4 = 2`
(ii) Number of students passed in Mathematics and Science but not in English.
i.e. `n(M nn S nn E') = n(M nn S) - n(M nn S nn E)`
` = 7 - 4 = 3`
(iii) Number of students passed in mathematics only
i.e., `n(M nn S' nn E') = n(M) - n(M nn S) - n(M nn E) + ( M nn S nn E)`
`= 12 - 7 - 6 + 4 = 3`
(iv) Number of students passed in more than one subjected only
i.e., `n(E nn M) + n(M nn S) + n(E nn S) - 3 n(E nn M nn S) + n(E nn M nn S)`
`= 6 + 7 + 4 - 4 xx 3 + 4`
`= 17 - 12 + 4 = 5 + 4 = 9`
