Text Solution
Verified by Experts
Topper's Solved these Questions
TRIANGLES
NCERT EXEMPLAR ENGLISH|Exercise Short Answer Type Questions|15 VideosTRIANGLES
NCERT EXEMPLAR ENGLISH|Exercise Long Answer Type Questions|18 VideosTRIANGLES
NCERT EXEMPLAR ENGLISH|Exercise Long Answer Type Questions|18 VideosSURFACE AREAS AND VOLUMES
NCERT EXEMPLAR ENGLISH|Exercise LONG ANSWER TYPE QUESTIONS|20 Videos
Similar Questions
Explore conceptually related problems
NCERT EXEMPLAR ENGLISH-TRIANGLES-Very Short Answer Typw Questions
- Is the triangle with sides 25 cm, 5 cm and 24 cm a right triangle? Giv...
Text Solution
|
- It is given that DeltaDEF~DeltaRPQ. Is it true to say that angleD = an...
Text Solution
|
- A and B are respectively the points on the sides PQ and PR of a Delta ...
Text Solution
|
- In figure BD and CE intersect each other at the point P. IsDeltaPBC~De...
Text Solution
|
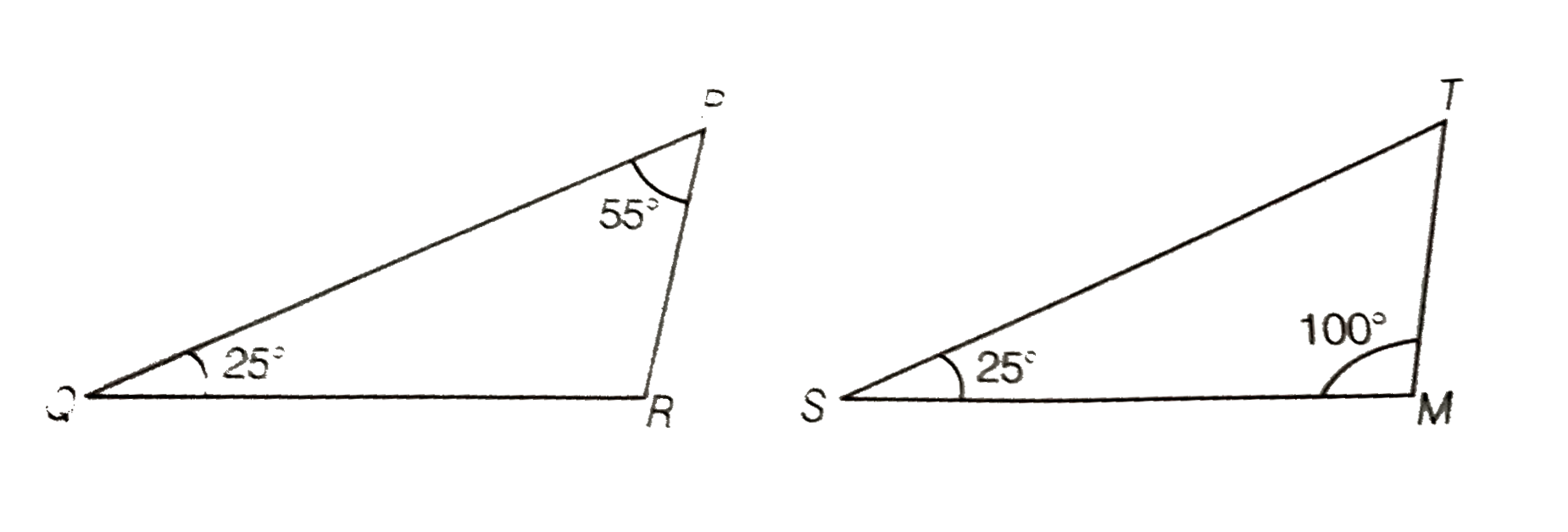
- In DeltaPQR and DeltaMST, angleP=55^(@),angleQ=25^(@),angleM=100^(@)an...
Text Solution
|
- Is the following statement true? Why? "Two quadrilaterals are similar,...
Text Solution
|
- Two sides and the perimeter of one triangle are respectively three tim...
Text Solution
|
- If in two right triangles, one of the acute angles of one triangle is ...
Text Solution
|
- The ratio of the corresponding altitudes of two similar triangles is 3...
Text Solution
|
- D is a point on side QR of DeltaPQR such that PDbotQR. Will it be corr...
Text Solution
|
- In figure, if angleD=angleC, then it is true that DeltaADE~DeltaACB? W...
Text Solution
|
- Is it true to say that, if in two triangles, an angle of one triangle ...
Text Solution
|