Home
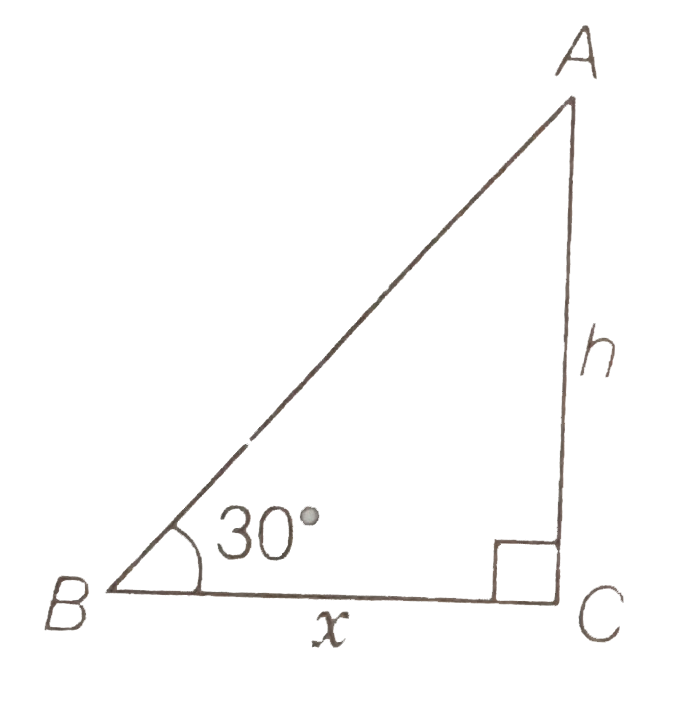
Class 10
MATHS
The angle of elevation theta of the top ...

The angle of elevation `theta` of the top of a tower is `30^(@)`. If the height of the tower is doubled, then new `tan theta` will be

A

`sqrt 3/2`

B

`3/2`

C

`2/3`

D

`2/sqrt 3`

Text Solution

Verified by Experts

The correct Answer is:
D
False,
Case I Let the height of the tower is h and BC = xm
In `DeltaABC`,
`tan30^(@)=(AC)/(BC) = h/x`
`rArr 1/sqrt(3) = h/x`………(i)
Case II By condition, the height of the tower is doubled, i.e., PR=2h.
In `DeltaPQR`, `tantheta=(PR)/(QR)=(2h)/x`
`rArr tantheta=2/x xx x/sqrt(3)` `[therefore h=x/sqrt(3)]`, from Eq. (i)
`rArr tantheta=2/sqrt(3) = 11.5`
`therefore theta=tan^(-1)(1.15) lt 60^(@)` M
Hence, the requried angle is not doubled.
Promotional Banner

Topper's Solved these Questions

  • INTRODUCTION TO TRIGoNOMETRY AND ITS APPLICATIONS

    NCERT EXEMPLAR ENGLISH|Exercise SHORT ANSWER TYPE QUESTIONS|15 Videos

  • INTRODUCTION TO TRIGoNOMETRY AND ITS APPLICATIONS

    NCERT EXEMPLAR ENGLISH|Exercise LONG ANSWER TYPES QUESTIONS|18 Videos

  • INTRODUCTION TO TRIGoNOMETRY AND ITS APPLICATIONS

    NCERT EXEMPLAR ENGLISH|Exercise LONG ANSWER TYPES QUESTIONS|18 Videos

  • COORDINATE GEOMETRY

    NCERT EXEMPLAR ENGLISH|Exercise Exercise 7.4 Long Answer Type Questions|6 Videos

  • PAIR OF LINEAR EQUATIONS IN TWO VARIABLES

    NCERT EXEMPLAR ENGLISH|Exercise Exercise 3.4 Long Answer Type Questions|13 Videos

Similar Questions

Explore conceptually related problems

Two men are on the opposite sides of a tower. They measure the angles of elevation of the top of the tower as 45^(@) and 30^(@) respectively. If the height of the tower is 40 m, then the distance between the men is

Two man are on the opposite sides of a tower. They measure the angles of elevation the top of the tower as 30^(@)" and "60^(@) . If the height of the tower is 150 m, find the distance between the two men.

The distance between two towers is 140 m while seeing from the top if the second tower, the angle of elevation of first tower is 30^(@) .If the height of the second tower is 60 m, then find the height of the first tower.

A T.V. Tower stands vertically on a bank of a river. From a point on the other bank directly opposite to the tower, the angle of elevation of the top of the tower is 60 degrees. From a point 20m away this point on the same bank, the angle of elevation of the top of the tower is 30o . Find the height of the tower and the width of the river.

From the top of a building 15m high the angle of elevation of the top of tower is found to be 30^@ . From the bottom of same building ; the angle of elevation of the top of the tower is found to be 60^@ . Find the height of the tower and the distance between tower and building .

A vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole the angle of elevation of the top of the tower is 60^(@) and the angle of depression of the bottom of the tower is 30^(@) . Find : the height of the tower, it the height of the pole is 20 m ,

The angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60^(@) and the angle of elevation of the top of the second tower from the foot of the first tower is 30^(@) . Find the distance between the two towers and also the height of the other tower.

The angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60^(@) and the angle of elevation of the top of the second tower from the foot of the first tower is 30^(@) . Find the distance between the two and also the height of the tower.

From the top of a 7 m high building, the angle of elevation of the top of a tower is 60° and the angle of depression of the foot of the tower is 30°. Find the height of the tower.

A person observed the angle of elevation of the top of a tower as 30^@ . He walked 50m towards the foot of the tower along level ground and found the angle of elevation of the top of the tower as 60^@ . Find the height of the tower.