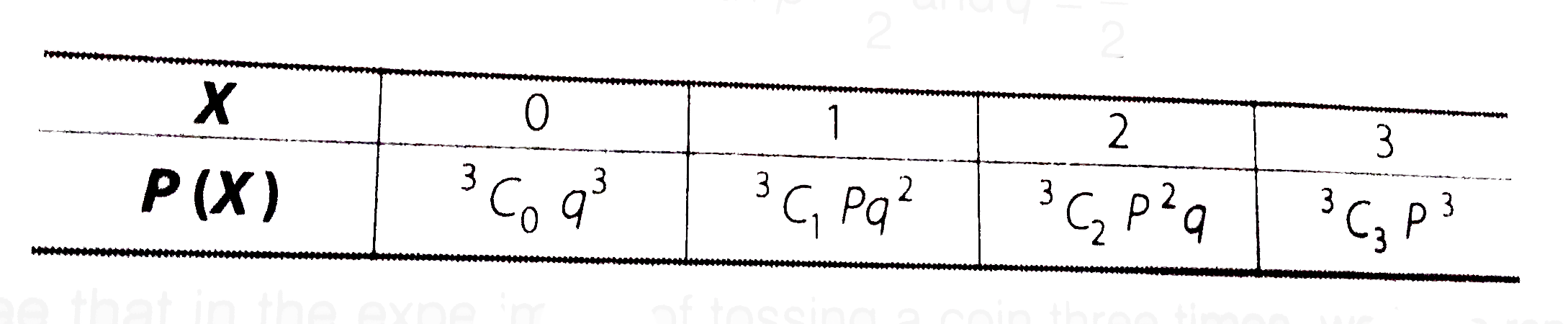Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT EXEMPLAR ENGLISH-PROBABILITY-True/False
- Explain why the experiment of tossing a coin three times is said to ha...
Text Solution
|
- Another name for the mean of a probability distribution is expected va...
Text Solution
|
- If A and B' are independent events, then P(A'cupB)=1-P(A)P(B').
Text Solution
|
- If A and B are two events suc that P(A)gt0 and P(A)+P(B)gt1, then P(B/...
Text Solution
|
- If A,B and C are three independent events such that P(A)=P(B)=P(C )=...
Text Solution
|
- If A and B are two events such that P(A/B)=p,P(A)=p,P(B)=1/3 and P(Acu...
Text Solution
|
- If A and B are such that P(A'cupB')=2/3andP(AcupB)=5/9 then P(A')+P(B'...
Text Solution
|
- If X follows Binomial distribution with parameters n=5, p and P(X=2)=9...
Text Solution
|
- If X be a random variable taking values x(1),x(2),x(3),….,x(n) with pr...
Text Solution
|
- Let A and B be two events. If P(A/B)=P(A), then A is …. of B
Text Solution
|