Text Solution
Verified by Experts
Topper's Solved these Questions
SAMPLE PAPER 2019
XII BOARD PREVIOUS YEAR PAPER ENGLISH|Exercise SECTION D|6 VideosSAMPLE PAPER 2019
XII BOARD PREVIOUS YEAR PAPER ENGLISH|Exercise SECTION B|9 VideosEXAM REVISION SERIES
XII BOARD PREVIOUS YEAR PAPER ENGLISH|Exercise All Questions|41 VideosXII BOARDS
XII BOARD PREVIOUS YEAR PAPER ENGLISH|Exercise SECTION - B|7 Videos
Similar Questions
Explore conceptually related problems
XII BOARD PREVIOUS YEAR PAPER ENGLISH-SAMPLE PAPER 2019-SECTION C
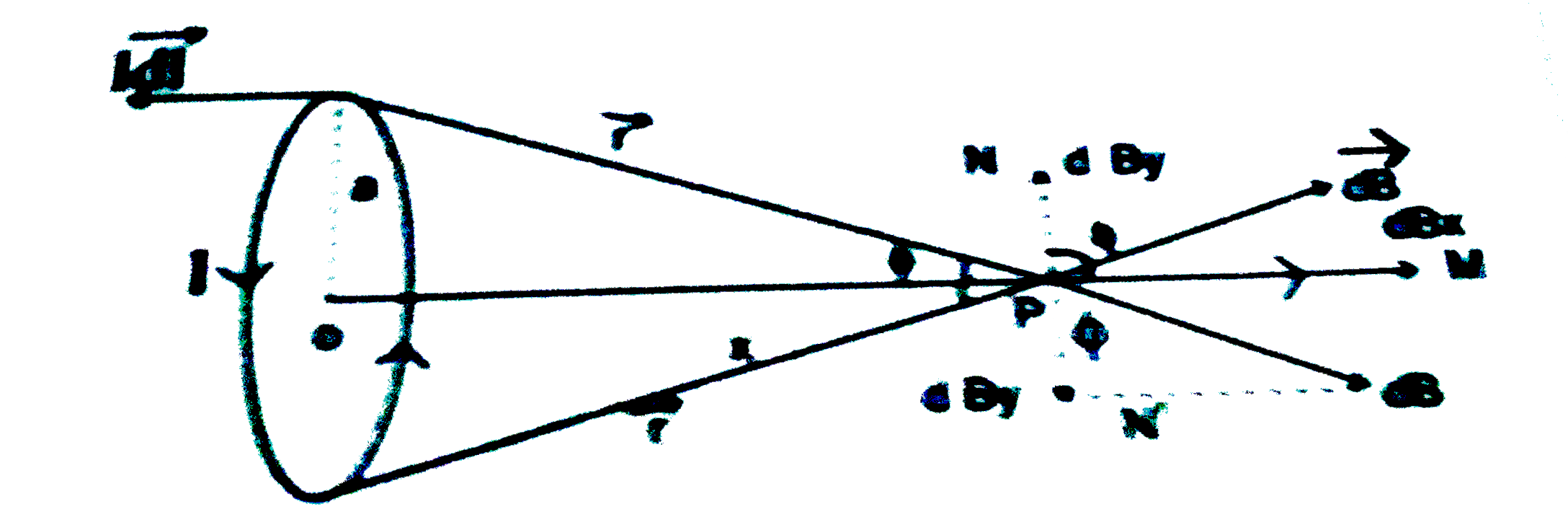
- State working principle of potentiometer. Explain how the balance poin...
Text Solution
|
- Using Biot-Savart’s law, derive an expression for magnetic field at an...
Text Solution
|
- Obtain the resonant frequency and Q – factor of a series LCR circuit w...
Text Solution
|
- State the conditions of total internal reflection. Refractive indices ...
Text Solution
|
- Define resolving power of an astronomical refracting telescope and wri...
Text Solution
|
- Write the basic assumptions used in the derivation of lens – maker’s f...
Text Solution
|
- Show that ""(92)^(238)U can not spontaneously emit a proton. Given: ...
Text Solution
|
- Suggest an idea to convert a full wave bridge rectifier to a half wave...
Text Solution
|