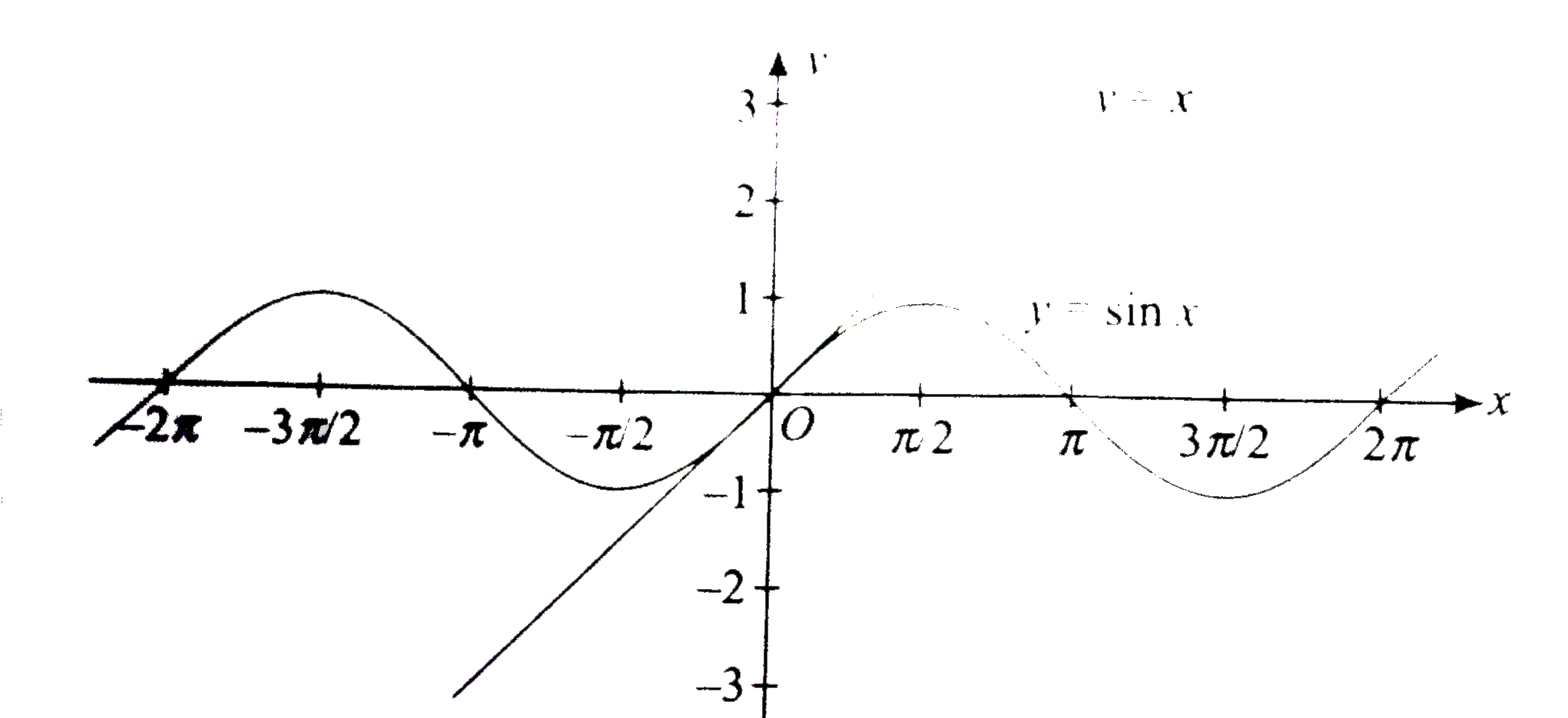Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE ENGLISH-LIMITS-Comprehension Type
- Prove that [lim(xto0) (sinx)/(x)]=0, where [.] represents the greatest...
Text Solution
|
- L=lim(xrarr0) (sin(sinx)-sinx)/(ax^(5)+bx^(3)+c)=-(1)/(12) The value...
Text Solution
|
- L=lim(xrarr0) (sin(sinx)-sinx)/(ax^(5)+bx^(3)+c)=-(1)/(12) The value...
Text Solution
|
- If f(x)=lim(nrarroo) ((x^(2)+ax+1)+x^(2n)(2x^(2)+x+b))/(1+x^(2n)) and ...
Text Solution
|
- If f(x)=lim(nrarroo)((x^(2)+ax+1)+x^(2n)(2x^(2)+x+b))/(1+x^(2n)) and l...
Text Solution
|