Home
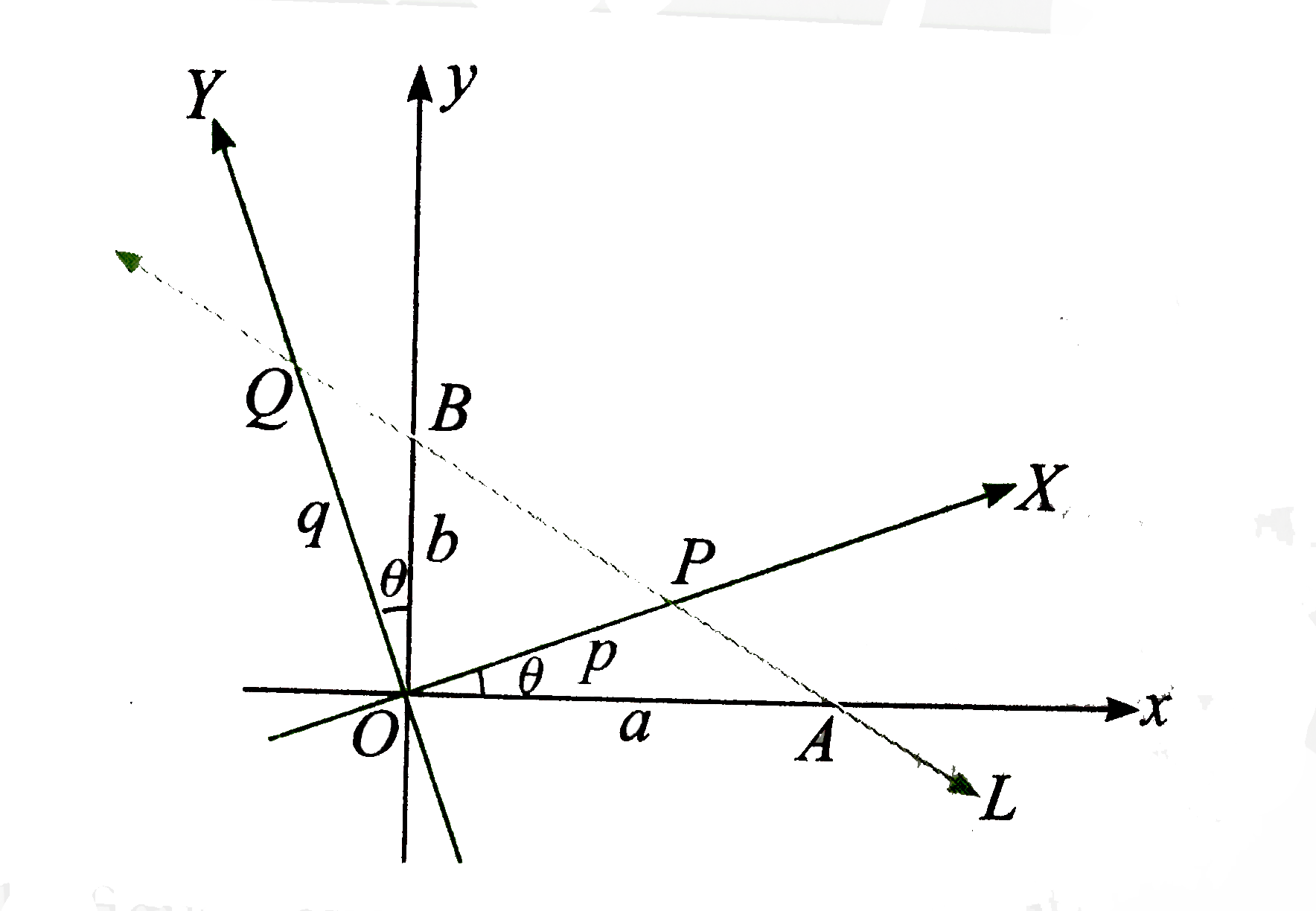
Class 12
MATHS
Line L has intercepts aa n db on the coo...

Line `L` has intercepts `aa n db` on the coordinate axes. When the axes are rotated through a given angle keeping the origin fixed, the same line `L` has intercepts `pa n dqdot` Then `a^2+b^2=p^2+q^2` `1/(a^2)+1/(b^2)=1/(p^2)+1/(q^2)` `a^2+p^2=b^2+q^2` (d) `1/(a^2)+1/(p^2)=1/(b^2)+1/(q^2)`

A

(a) `a^2+b^2=p^2+q^2`

B

(b) `1/(a^2)+1/(b^2)=1/(p^2)+1/(q^2)`

C

(c) `a^2+p^2=b^2+q^2`

D

(d) `1/(a^2)+1/(p^2)=1/(b^2)+1/(q^2)`

Text Solution

Verified by Experts


As shown in the figure, axes are rotated by an angle `theta` about origin in anticlockwise direction.
Line L has intercepts a and b on original axes and intercepts p and q on rotated axes.
Equation of line L w.r.t. original axes is
`(x)/(a) + (y)/(b)-1= 0 " " (1)`
Equation of line L w.r.t. rotated axes is
`(x)/(p) + (y)/(q)-1= 0 " " (2)`
Since origin and line L are not changing their positions, distance of line from origin remains the same even though the axes are rotated.
So, comaring distances of lines given by equations (1) and (2) from origin, we get
`(|(0)/(a) + (0)/(b)-1|)/(sqrt((1)/(a^(2))+ (1)/(b^(2)))) = (|(0)/(p) + (0)/(q)-1|)/(sqrt((1)/(p^(2))+ (1)/(q^(2))))`
`rArr (1)/(a^(2)) + (1)/(b^(2)) = (1)/(p^(2)) + (1)/(q^(2))`
Promotional Banner

Topper's Solved these Questions

  • STRAIGHT LINES

    CENGAGE ENGLISH|Exercise EXAMPLE|12 Videos

  • STRAIGHT LINES

    CENGAGE ENGLISH|Exercise CONCEPT APPLICATION EXERCISE 2.1|23 Videos

  • STRAIGHT LINE

    CENGAGE ENGLISH|Exercise Multiple Correct Answers Type|8 Videos

  • THEORY OF EQUATIONS

    CENGAGE ENGLISH|Exercise JEE ADVANCED (Numerical Value Type )|1 Videos

Similar Questions

Explore conceptually related problems

Line L has intercepts aa n db on the coordinate axes. When the axes are rotated through a given angle keeping the origin fixed, the same line L has intercepts pa n dqdot Then (a) a^2+b^2=p^2+q^2 (b) 1/(a^2)+1/(b^2)=1/(p^2)+1/(q^2) (c) a^2+p^2=b^2+q^2 (d) 1/(a^2)+1/(p^2)=1/(b^2)+1/(q^2)

Line L has intercepts a and b on the coordinate axes. When the axes are rotated through a given angle keeping the origin fixed, the same line L has intercepts p and qdot Then (a) a^2+b^2=p^2+q^2 (b) 1/(a^2)+1/(b^2)=1/(p^2)+1/(q^2) (c) a^2+p^2=b^2+q^2 (d) 1/(a^2)+1/(p^2)=1/(b^2)+1/(q^2)

If p is the length of perpendicular from the origin to the line whose intercepts on the axes are a and b, then show that 1/(p^2)=1/(a^2)+1/(b^2) .

If p is the length of perpendicular from the origin to the line whose intercepts on the axes are a and b, then show that 1/(p^2)=1/(a^2)+1/(b^2) .

If p is the perpendicualr distance of the origin from the line whose intercepts on the axes are a and b, show that 1/(p^(2))=1/(a^(2))+1/(b^(2))

If p is the length of perpendicular from the origin to the line whose intercepts on the axes are a and b, then show that 1/(p^2)=1/(a^2)+1/(b^2) .

If p be the length of the perpendicular from the origin on the line x//a+y//b =1, then p^2=a^2+b^2 b. p^2=1/(a^2)+1/(b^2) c. 1/(p^2)=1/(a^2)+1/(b^2) d. none of these

If a plane has intercepts a, b and c on the coordinate axes and is at a distance of p units from the origin, prove that they (1)/(a^(2))+(1)/(b^(2))+(1)/(c^(2))=(1)/(p^(2))

Prove that if a plane has the intercepts a, b, c and is at a distance of p units from the origin, then 1/(a^2)+1/(b^2)+1/(c^2)=1/(p^2) .

Given that tanalpha and tanbeta,x^2-p x+q=0 , then value of sin^2(alpha+beta)= (p^2)/(p^2+(1-q)^2) (b) (p^2)/(p^2+q^2) (q^2)/(p^2+(1-q)^2) (d) (p^2)/((p+q)^2)