A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE ENGLISH-COMPLEX NUMBERS-MATRIX MATCH TYPE
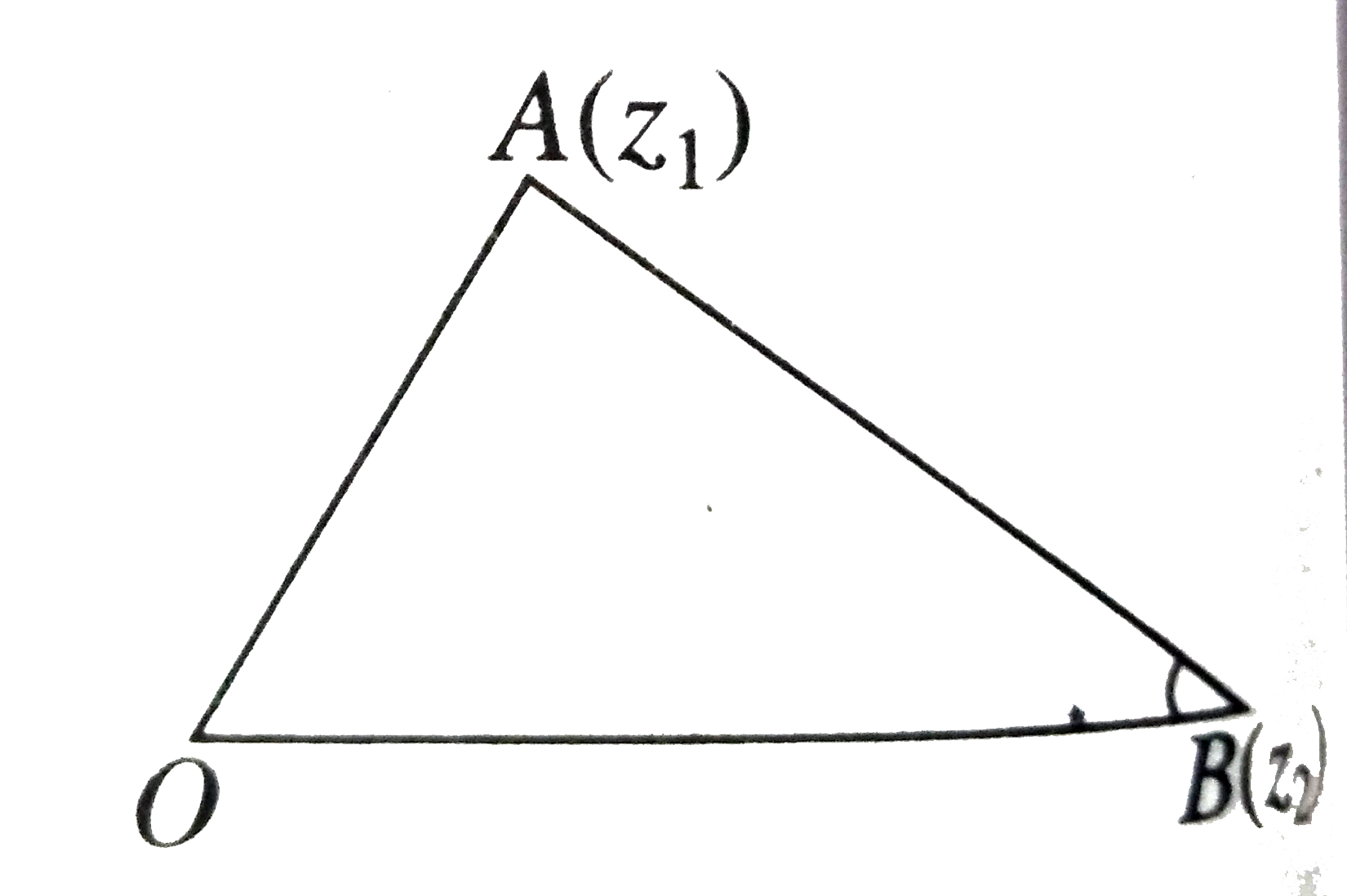
- Let A(z(1)) and B(z(2)) are two distinct non-real complex numbers in t...
Text Solution
|
- The graph of the quadrationc funtion y =ax^(2) + bx + c is as shown in...
Text Solution
|
- Let z(1),z(2) and z(3) be the vertices of trinagle . Then match follo...
Text Solution
|
- Match the following lists:
Text Solution
|
- Complex number z satisfies the equation ||z-5i| + m|z-12i||=n. Then ma...
Text Solution
|
- Complex number z lies on the curve S-= arg(z+3)/(z+3i) =-(pi)/(4)
Text Solution
|
- Consider sets A = {z in C: z^(27) - 1=0} and B = { z in C: z^(36) - 1=...
Text Solution
|
- Match the statements in List I with those in List II [Note: Here z ...
Text Solution
|
- Let z(k) = cos((2kpi)/(10)) -isin ((2kpi)/(10)), k = 1,2,…..,9
Text Solution
|
- Match the conics in List I with the statements/expressions in List II
Text Solution
|