The given curves are `y=x^(2)" (1)"`
`and" "y=(2)/(1+x^(2))" (2)"`
Solving (1) and (2), we have
`x^(2)=(2)/(1+x^(2))`
`"or "x^(4)+x^(2)-2=0`
`"or "(x^(2)-1)(x^(2)+2)=0`
`"or "(x^(2)-1)(x^(2)+2)=0`
`"or "x=pm 1`
`"Also, "y=(2)/(1+x^(2))` is an even function.
Hence, its graph is symmetrical about y-axis.
At x = 0, y = 2, by increasing the values of x,y decreases and when `xrarroo,yrarr0.`
Therefore, y=0 is an asymptote of the given curve.
Thus, the graphs of the two curves are as follows :
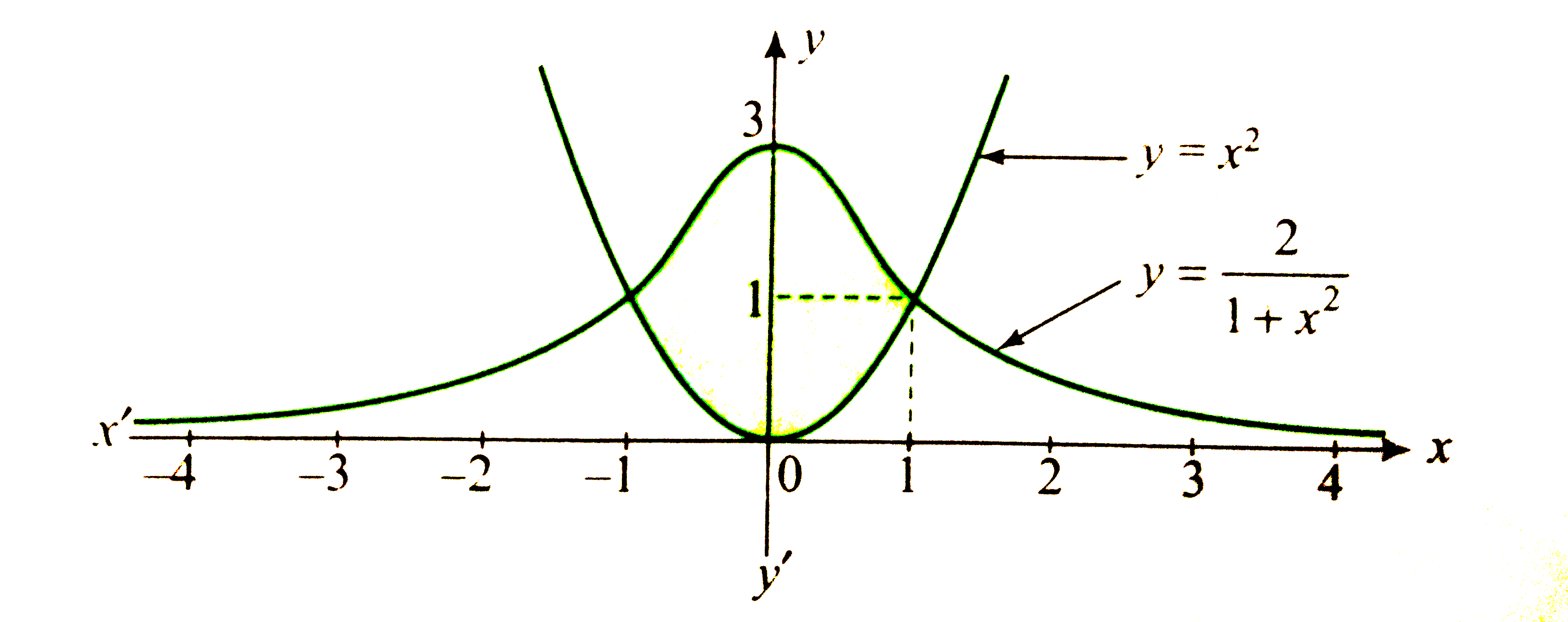
`"Required area "=2int_(0)^(1)((2)/(1+x^(2))-x^(2))dx`
`=(4 tan^(-1)x-(2x^(3))/(3))_(0)`
`=pi-(2)/(3)` sq. units.