Text Solution
Verified by Experts
Topper's Solved these Questions
AREA
CENGAGE ENGLISH|Exercise Concept Application Exercise 9.1|9 VideosAREA
CENGAGE ENGLISH|Exercise Concept Application Exercise 9.2|14 VideosAREA
CENGAGE ENGLISH|Exercise Comprehension Type|2 VideosAPPLICATIONS OF DERIVATIVES
CENGAGE ENGLISH|Exercise Comprehension Type|5 VideosBINOMIAL THEOREM
CENGAGE ENGLISH|Exercise Matrix|4 Videos
Similar Questions
Explore conceptually related problems
CENGAGE ENGLISH-AREA-Solved Examples
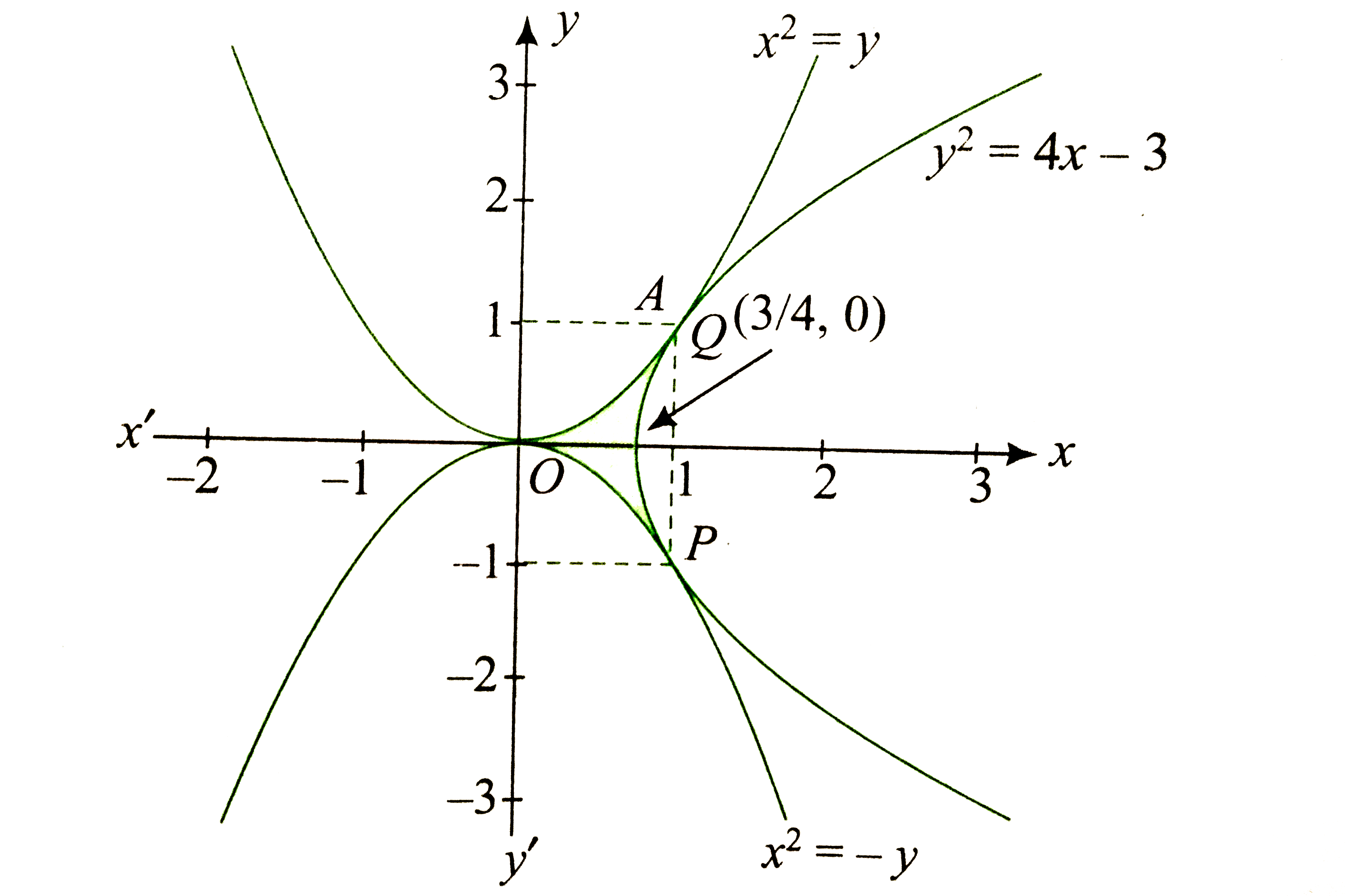
- Find the area bounded by the curve x^2=y ,x^2=-ya n dy^2=4x-3
Text Solution
|
- Find the area of the region enclosed by the curve y=|x-(1)/(x)|(xgt0) ...
Text Solution
|
- Find the area of the region bounded by the curves y=x^2,y=|2-x^2|,a n ...
Text Solution
|
- The ratio in which the line x-1=0 divides the area bounded by the curv...
Text Solution
|
- If S(0),S(1),S(2),… are areas bounded by the x-axis and half-wave of t...
Text Solution
|
- Find the area of the figure enclosed by the curve 5x^2+6x y+2y^2+7x+6y...
Text Solution
|
- Find the area bounded by the curves x^2+y^2=4, x^2=-sqrt2 y and x=y
Text Solution
|
- Find the area of the region bounded by the curve C : y=tanx ,t a nge n...
Text Solution
|
- Compute the area of the region bounded by the curves y-e x(log)e xa n ...
Text Solution
|
- If An be the area bounded by the curve y=(tanx)^n and the lines x=0,\ ...
Text Solution
|