`"For "yge sqrt(1-x^(2))`
points lie outside circle `x^(2)+y^(2)=1" for "yge 0 and -1 le xle 1.`
`"For "max {|x|,|y|}le4," where have"`
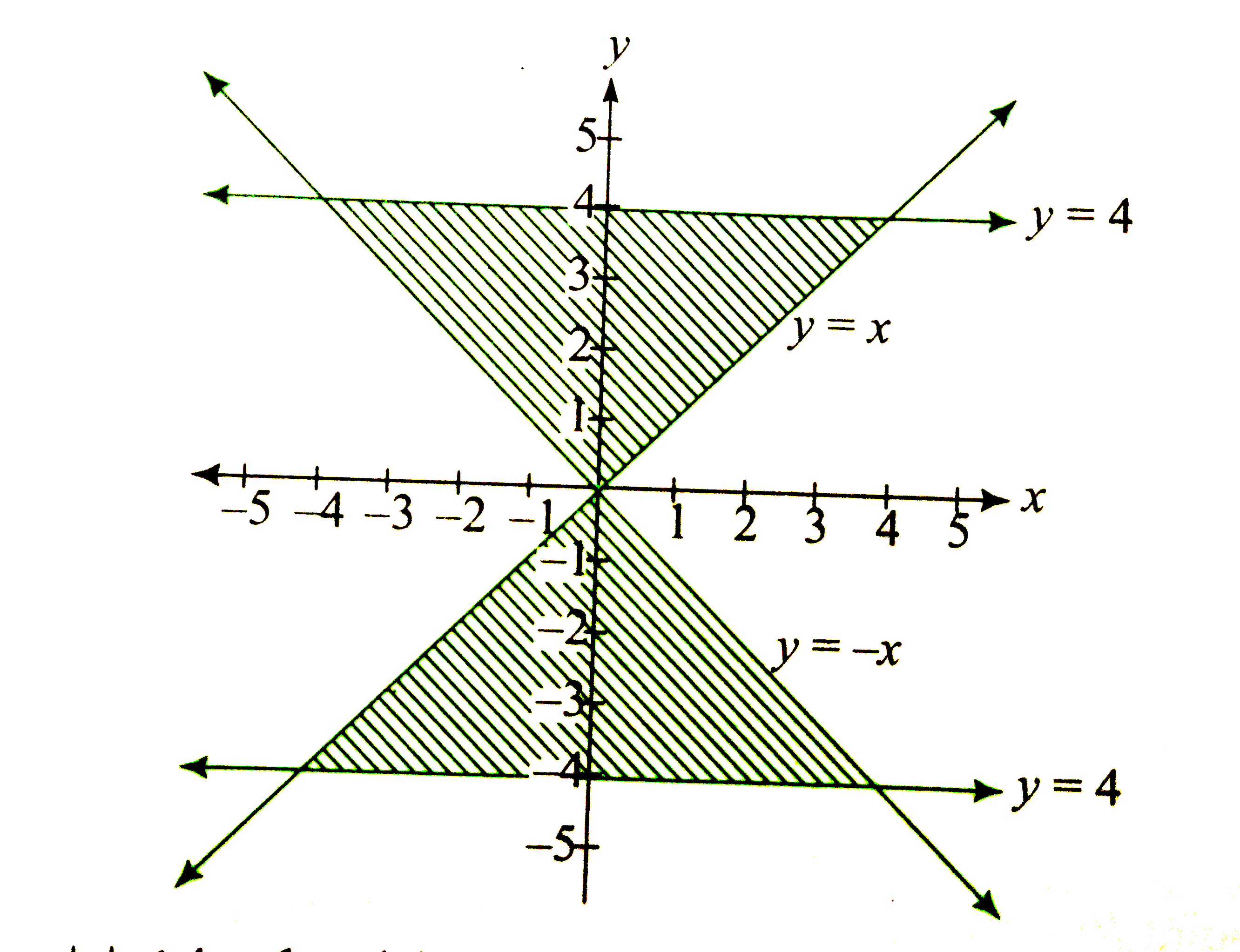
`|y|le4," when "|x|lt|y|" (2)"`
The points satisfying above inequalities from region as shown in the figure.
`|x|le4," when "|y|lt|x|" (3)"`
The points satisfying above inequalities from region as shown in the figure.
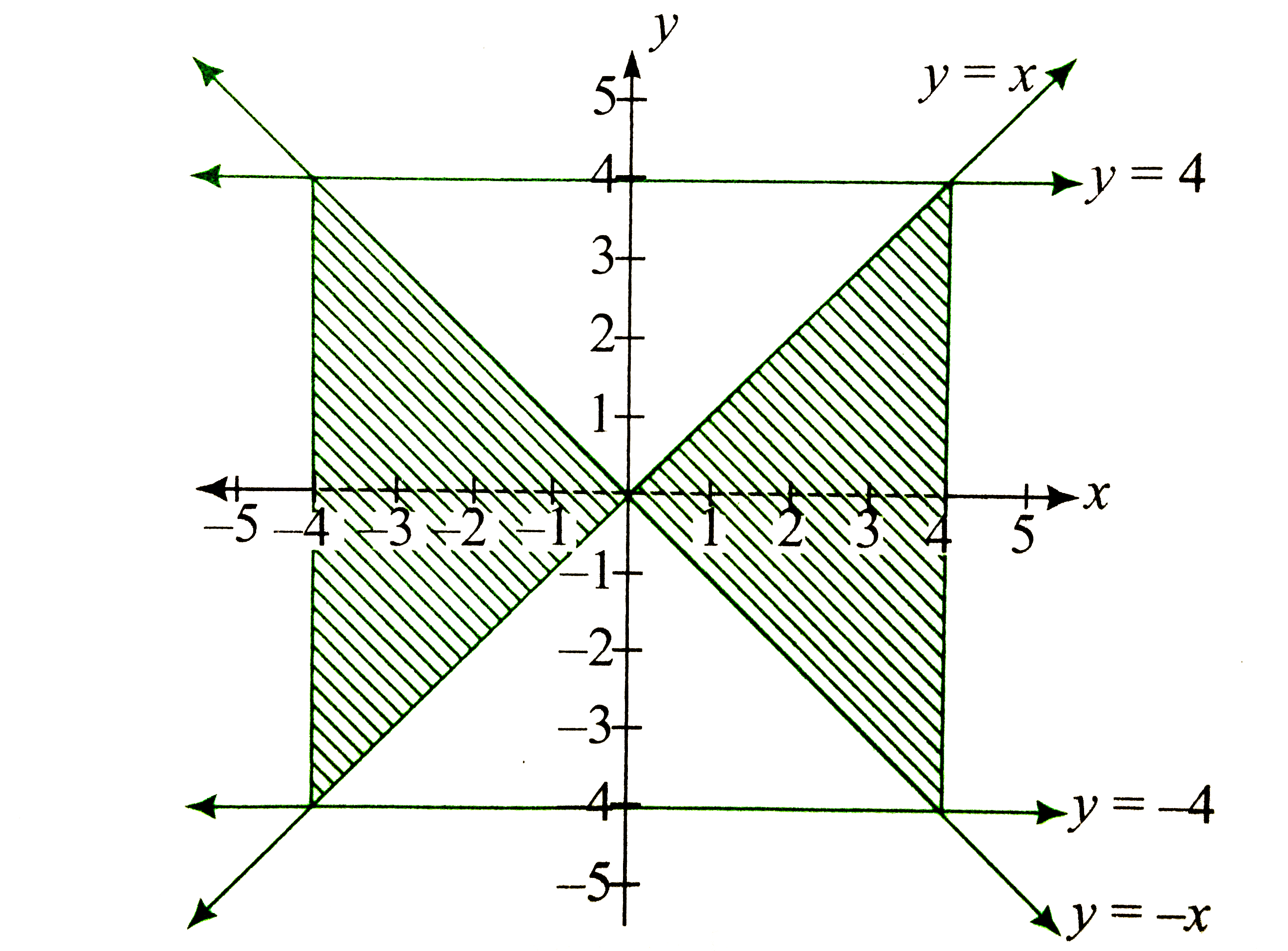
The region `(1) cap(2)cup(3))` is as shown in the figure.
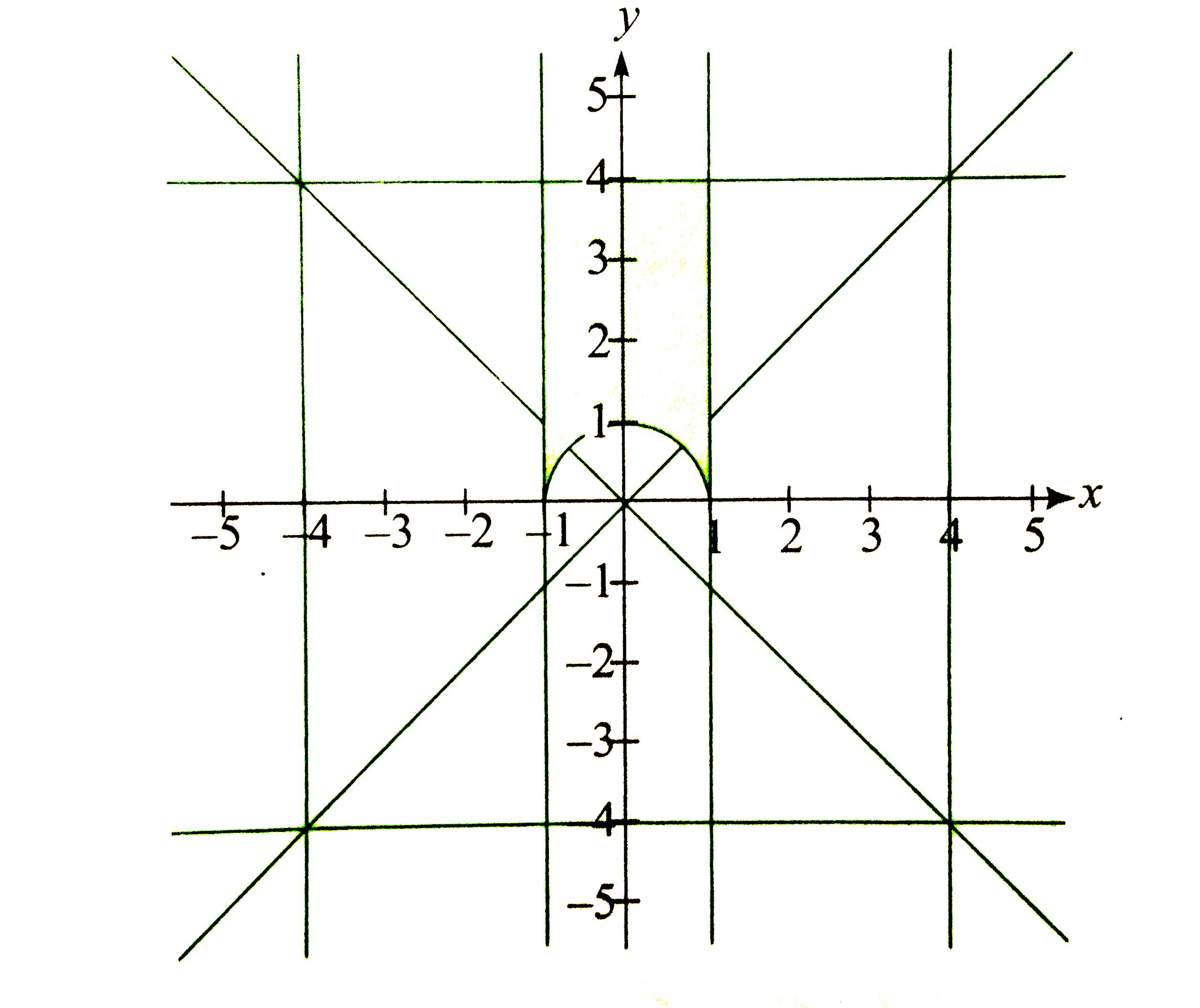
From the figure, required area is
=Area of rectangle- Area of semicircle having radius 1
`=8-(pi)/(2)`