Home
Class 12
MATHS
Plot the region in the first quadrant in...

Plot the region in the first quadrant in which points are nearer to the origin than to the line `x=3.`

Text Solution

Verified by Experts

Point P(x,y) lies in the first quadrant. Therefore, `x,ygt0`

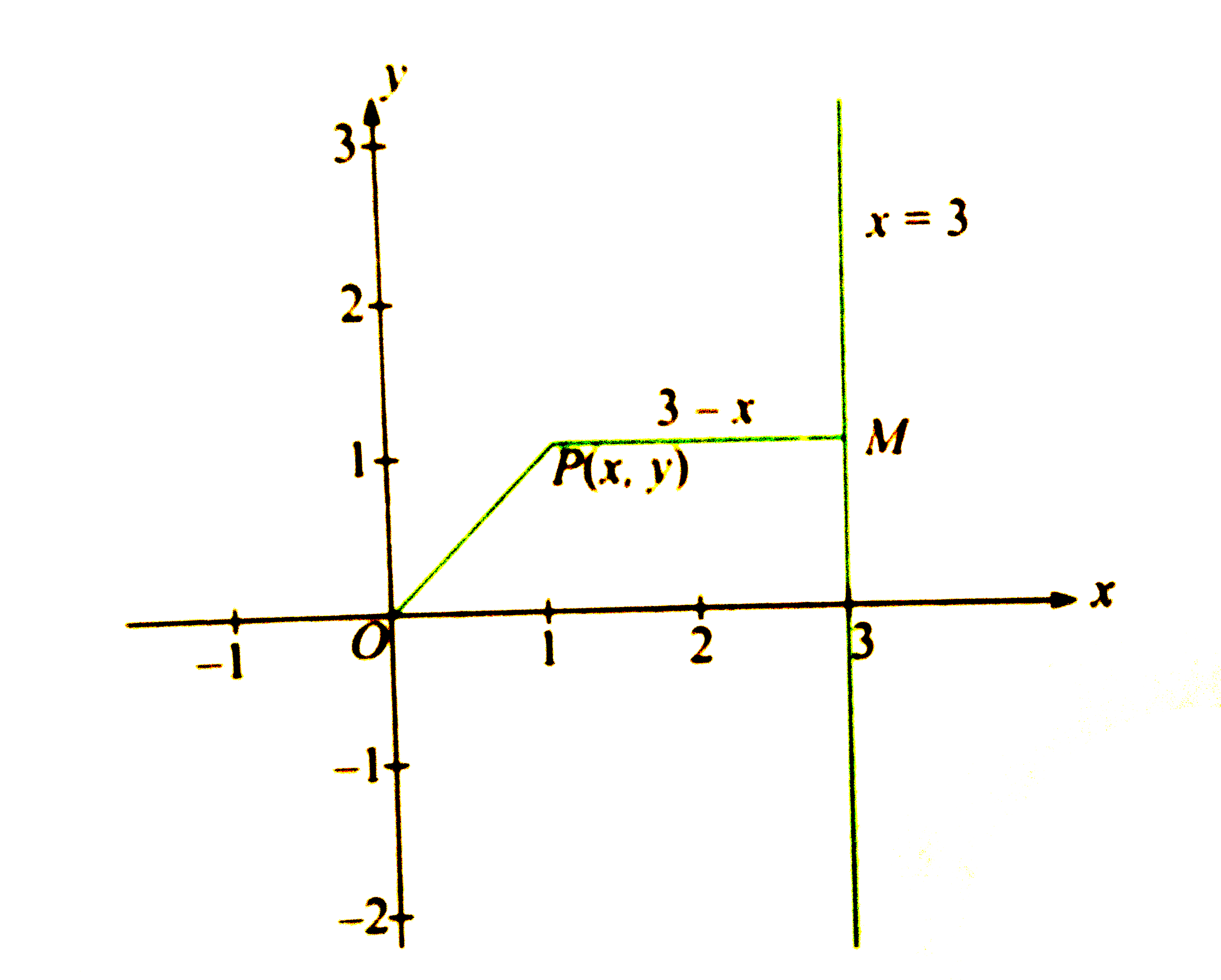
Also point P(x,y) is nearer to the origin than to the line x=3
`"Now "OP=sqrt(x^(2)+y^(2))`
Distance of P from line x-3=0 is PM =3-x
According to the question, `OPltPM`
`rArr" "sqrt(x^(2)+y^(2))lt(3-x)`
`"or "x^(2)+y^(2)ltx^(2)-6x+9`
`"or "y^(2)lt-6x+9`
`"or "y^(2)lt-6(x-(3)/(2))`
Points satisfying above inequality lie inside parabola `y^(2)=9-6x` in the first quadrant.
`"Parabola "y^(2)=-6(x-(3)/(2))` is concave to the left, having axis as
x-axis and vertex at `((3)/(2),0)` and directrix x=3
The required region as shown in the figure.

`"Area of the region "=overset(3)underset(0)int(9-y^(2))/(6)dy=(1)/(6)(9y-(y^(3))/(3))_(0)^(3)`
`=(1)/(6)(27-9)=3` sq. units
Promotional Banner

Topper's Solved these Questions

  • AREA

    CENGAGE ENGLISH|Exercise Solved Examples|10 Videos

  • AREA

    CENGAGE ENGLISH|Exercise Concept Application Exercise 9.1|9 Videos

  • APPLICATIONS OF DERIVATIVES

    CENGAGE ENGLISH|Exercise Comprehension Type|5 Videos

  • BINOMIAL THEOREM

    CENGAGE ENGLISH|Exercise Matrix|4 Videos

Similar Questions

Explore conceptually related problems

Consider a square with vertices at (1,1)(-1,1)(-1,-1)and(1,-1). Let S be the region consisting of all points inside the square which are nearer to the origin than to any edge. Sketch the region S and find its area.

Consider a square with vertices at (1,1),(-1,1),(-1,-1),a n d(1,-1)dot Set S be the region consisting of all points inside the square which are nearer to the origin than to any edge. Sketch the region S and find its area.

Consider a square with vertices at (1,1),(-1,1),(-1,-1),a n d(1,-1)dot Set S be the region consisting of all points inside the square which are nearer to the origin than to any edge. Sketch the region S and find its area.

In which quadrant do the points lie: (4,3)

Find the area of the region in the first quadrant enclosed by the y-axis, the line y=x and the circle x^2+y^2=32 , using integration.

Find the point on the straight line 2x+3y=6 , which is closest to the origin.

Area of the region in the first quadrant exclosed by the X-axis, the line y=x and the circle x^(2)+y^(2)=32 is

Find the area of the region in the first quadrant enclosed by x-axis, the line y=sqrt(3\ )x and the circle x^2+y^2=16

Find the area of the region in the first quadrant enclosed by the x-axis, the line y" "=" x" , and the circle x^2+y^2=32 .

What is the number of square units in the area of the region in the first quadrant of the xy-plane that is bounded by y=|x|+2 , the line x=5, the positive x-axis, ant the positive y-axis?