Text Solution
Verified by Experts
Topper's Solved these Questions
CIRCLE
CENGAGE ENGLISH|Exercise CONCEPT APPLICATION EXERCISE 4.1|1 VideosCIRCLE
CENGAGE ENGLISH|Exercise CONCEPT APPLICATION EXERCISE 4.2|2 VideosCIRCLE
CENGAGE ENGLISH|Exercise MATRIX MATCH TYPE|7 VideosBINOMIAL THEOREM
CENGAGE ENGLISH|Exercise Matrix|4 VideosCIRCLES
CENGAGE ENGLISH|Exercise Comprehension Type|8 Videos
Similar Questions
Explore conceptually related problems
CENGAGE ENGLISH-CIRCLE -Examples
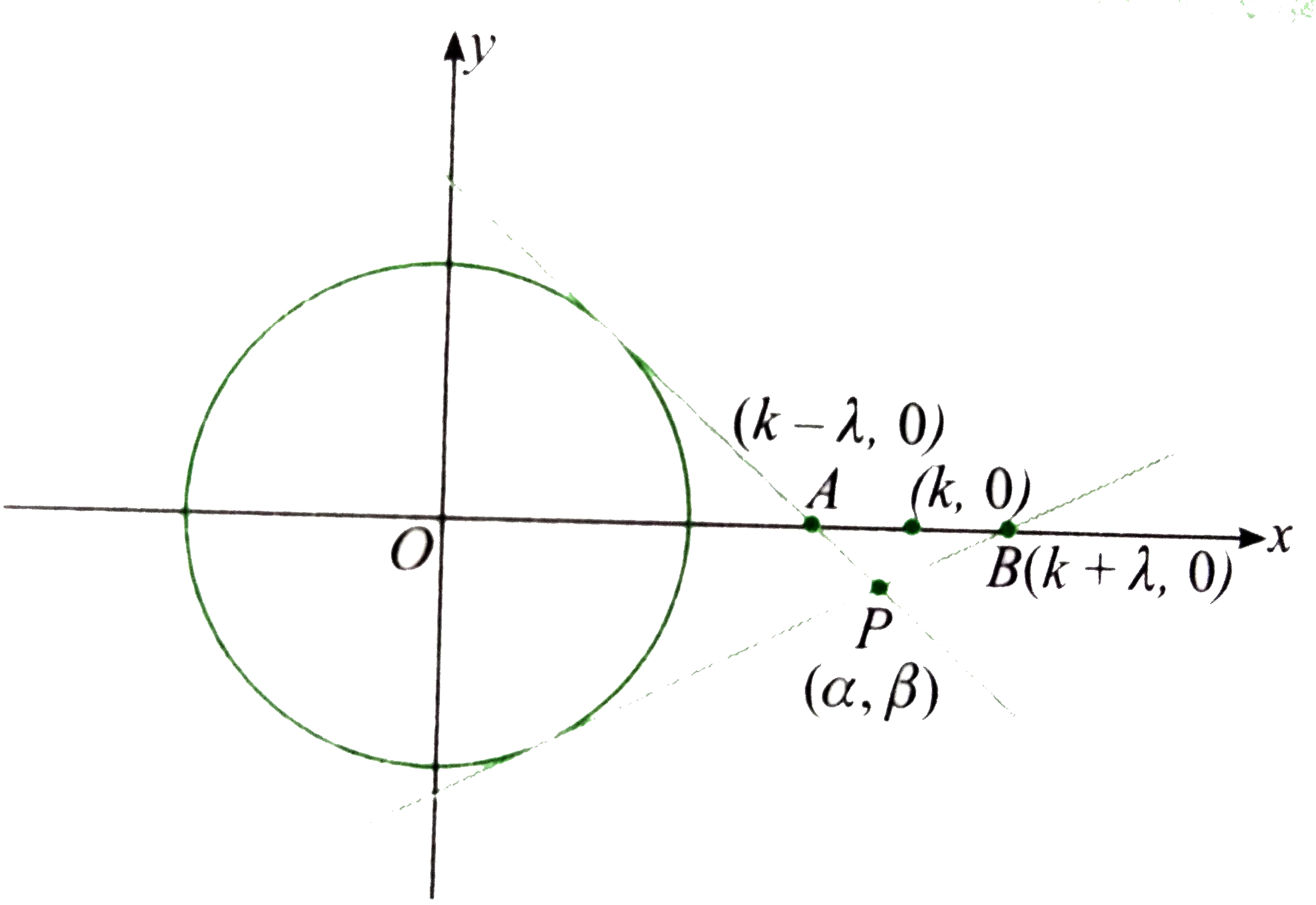
- The line A x+B y+C=0 cuts the circle x^2+y^2+a x+b y+c=0 at Pa n dQ . ...
Text Solution
|
- Tangents are drawn to the circle x^2+y^2=a^2 from two points on the ax...
Text Solution
|
- Lines 5x + 12y - 10 = 0 and 5x - 12y - 40 = 0 touch a circle C1 of dia...
Text Solution
|
- If eight distinct points can be found on the curve |x|+|y|=1 such that...
Text Solution
|
- Let A B be chord of contact of the point (5,-5) w.r.t the circle x^2+y...
Text Solution
|
- Let P be any moving point on the circle x^2+y^2-2x=1. A B be the chord...
Text Solution
|
- Aa n dB are two points in the xy-plane, which are 2sqrt(2) units dista...
Text Solution
|
- about to only mathematics
Text Solution
|
- Let S-=x^2+y^2+2gx+2f y+c= be a given circle. Find the locus of the fo...
Text Solution
|
- Let a circle be given by 2x(x-1)+y(2y-b)=0,(a!=0,b!=0) . Find the cond...
Text Solution
|
- about to only mathematics
Text Solution
|
- For the circle x^(2)+y^(2)=r^(2), find the value of r for which the ar...
Text Solution
|
- A circle of radius 1 unit touches the positive x-axis and the positive...
Text Solution
|