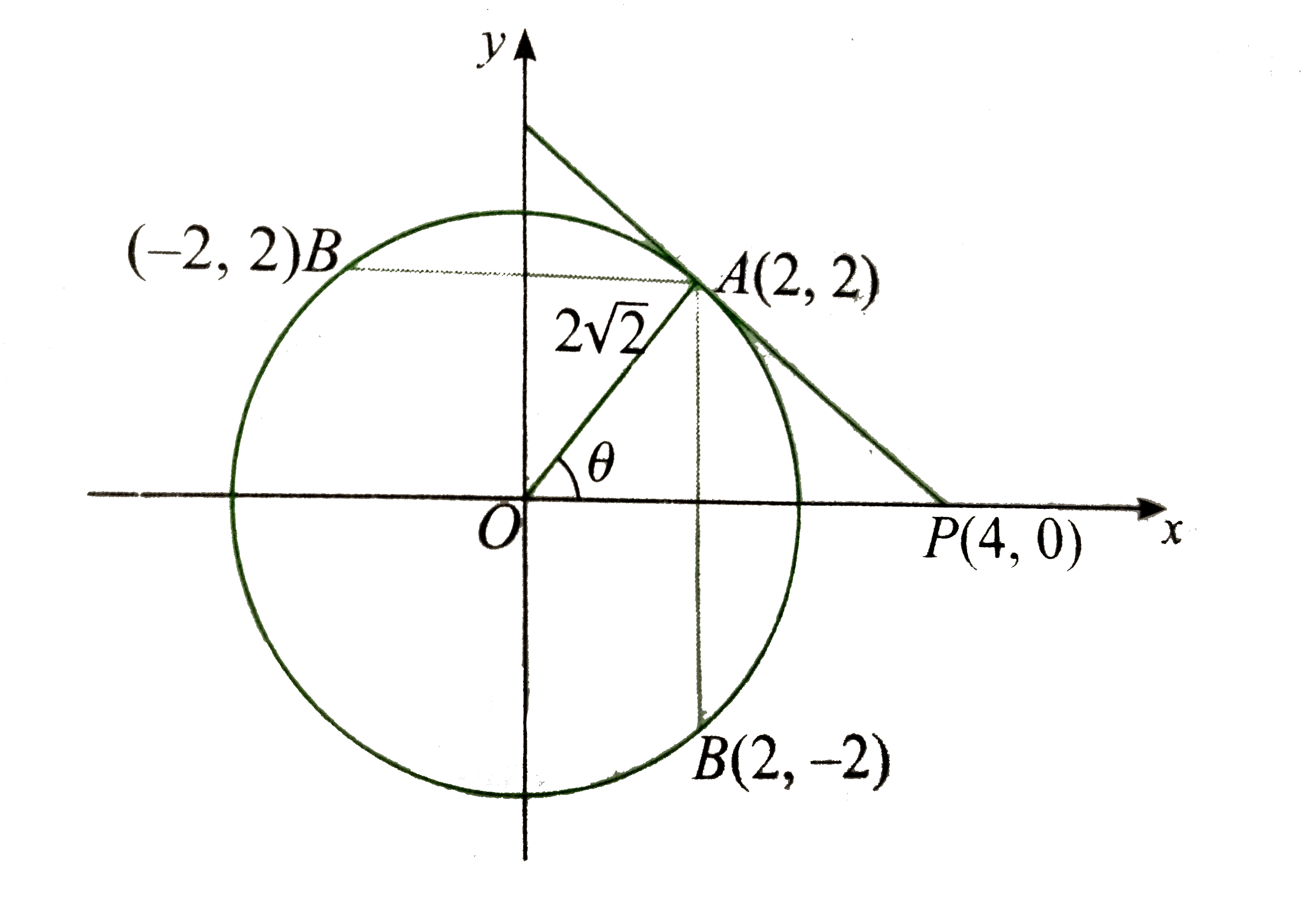Home
Class 12
MATHS
Tangent drawn from the point P(4,0) to t...

Tangent drawn from the point `P(4,0)` to the circle `x^2+y^2=8` touches it at the point `A` in the first quadrant. Find the coordinates of another point `B` on the circle such that `A B=4` .

Text Solution

Verified by Experts

The correct Answer is:
`(2,-2)` or (-2,2)
`cos theta=(2sqrt(2))/(4)=(1)/(sqrt(2))`
`theta=45^(@)`
`:. A-= (2,2)`
Let `B -= (x_(1),y_(1))`

Given AB =4 . Therefore,
`(x_(1)-2)^(2)+(y_(1)-2)^(2)=16`
or `x_(1)^(2)+y_(1)^(2)-4x_(1)-4y_(1)=8`
Also, `x_(1)^(2)+y_(1)^(2)=8`
`:. x_(1)+y_(1)=0`
`:. 2x_(1)^(2)=8`
or `x_(1) +- 2`
`:. B -= (2,-2) ` or `(-2,2)`
Promotional Banner

Topper's Solved these Questions

  • CIRCLE

    CENGAGE ENGLISH|Exercise CONCEPT APPLICATION EXERCISE 4.8|5 Videos

  • CIRCLE

    CENGAGE ENGLISH|Exercise CONCEPT APPLICATION EXERCISE 4.9|5 Videos

  • CIRCLE

    CENGAGE ENGLISH|Exercise CONCEPT APPLICATION EXERCISE 4.6|6 Videos

  • BINOMIAL THEOREM

    CENGAGE ENGLISH|Exercise Matrix|4 Videos

  • CIRCLES

    CENGAGE ENGLISH|Exercise Comprehension Type|8 Videos

Similar Questions

Explore conceptually related problems

Tangents drawn from (2, 0) to the circle x^2 + y^2 = 1 touch the circle at A and B Then.

Tangents drawn from the point (4, 3) to the circle x^(2)+y^(2)-2x-4y=0 are inclined at an angle

Tangents are drawn from the point P(3,4) to the ellipse x^(2)/9+y^(2)/4=1 touching the ellipse at point A and B. Q. The coordinates of A and B are

Tangents drawn from the point P(1,8) to the circle x^2 +y^2 -6x -4y-11=0 touch the circle at the points A&B ifR is the radius of circum circle of triangle PAB then [R]-

Tangents are drawn from the point P(3,4) to the ellipse x^(2)/9+y^(2)/4=1 touching the ellipse at point A and B. Q. The orthocenter of the trianlge PAB is

To the circle x^(2)+y^(2)+8x-4y+4=0 tangent at the point theta=(pi)/4 is

The point of contact of a tangent from the point (1, 2) to the circle x^2 + y^2 = 1 has the coordinates :

Tangents are drawn from the points on the line x-y-5=0 to x^2+4y^2=4 . Then all the chords of contact pass through a fixed point. Find the coordinates.

Tangents are drawn from the point P(1,-1) to the circle x^2+y^2-4x-6y-3=0 with centre C, A and B are the points of contact. Which of the following are correct?

Tangents drawn from P(1, 8) to the circle x^2 +y^2 - 6x-4y - 11=0 touches the circle at the points A and B, respectively. The radius of the circle which passes through the points of intersection of circles x^2+y^2 -2x -6y + 6 = 0 and x^2 +y^2 -2x-6y+6=0 the circumcircle of the and interse DeltaPAB orthogonally is equal to