Home
Class 12
MATHS
Two variable chords A Ba n dB C of a cir...

Two variable chords `A Ba n dB C` of a circle `x^2+y^2=r^2` are such that `A B=B C=r` . Find the locus of the point of intersection of tangents at `Aa n dCdot`

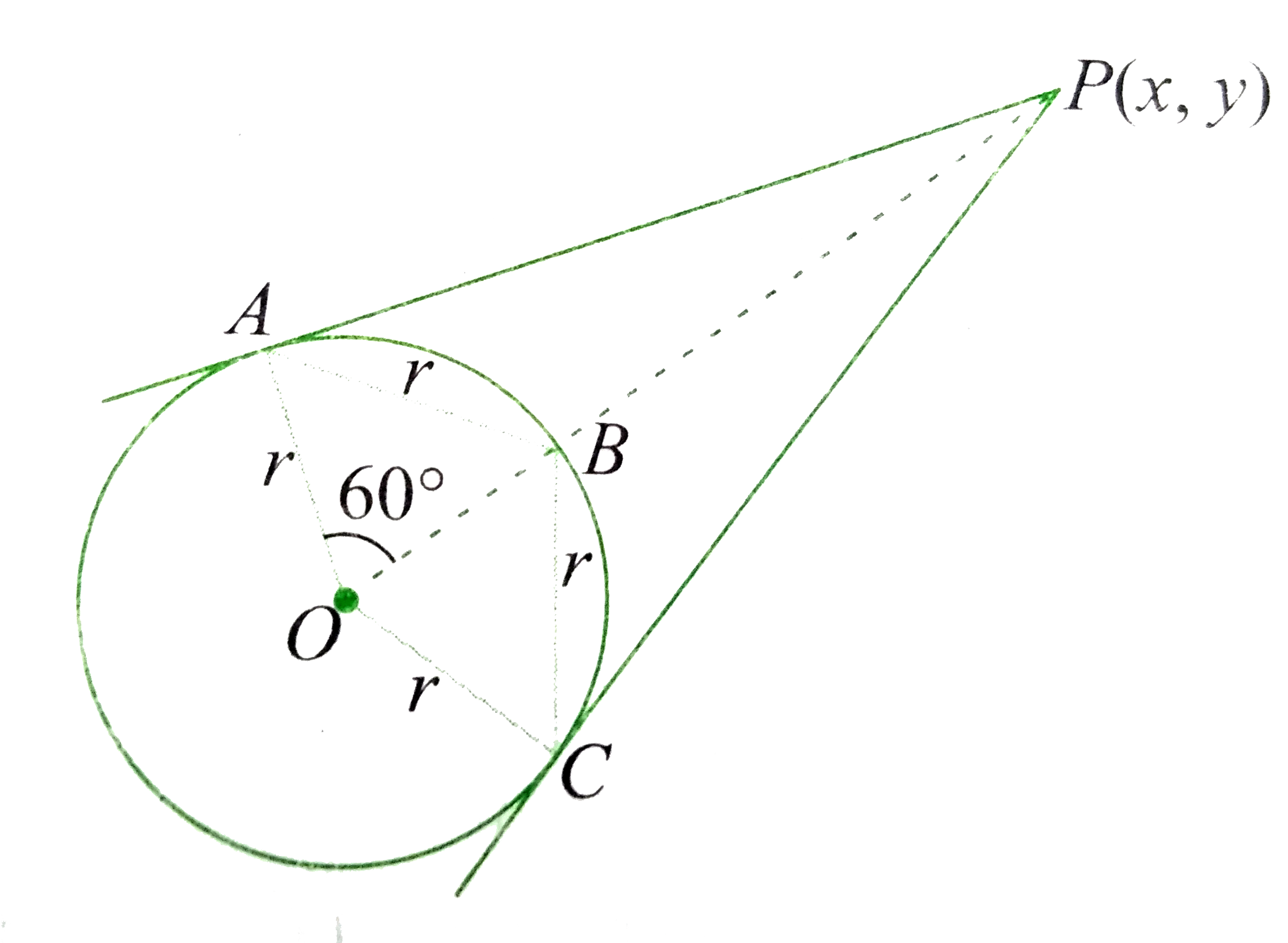
Text Solution

Verified by Experts

The correct Answer is:
`x^(2)+y^(2)=4r^(2)`
Let the point of intersection of tangents at A and be `P -= (x,y)` .
Since `AB =AO =BO =r`, we get
`/_ AOB =60^(@)`

or `(PA)/(r) tan 60^(@) = sqrt (3)`
or `sqrt(x^(2)+y^(2)-r^(2))=sqrt(3)r`
Therefore, `x^(2)+y^(2)=4r^(2)` is the locus of the point P.
Doubtnut Promotions Banner Mobile Dark
|

Topper's Solved these Questions

  • CIRCLE

    CENGAGE ENGLISH|Exercise CONCEPT APPLICATION EXERCISE 4.16|3 Videos

  • CIRCLE

    CENGAGE ENGLISH|Exercise CONCEPT APPLICATION EXERCISE 4.17|2 Videos

  • CIRCLE

    CENGAGE ENGLISH|Exercise CONCEPT APPLICATION EXERCISE 4.14|4 Videos

  • BINOMIAL THEOREM

    CENGAGE ENGLISH|Exercise Matrix|4 Videos

  • CIRCLES

    CENGAGE ENGLISH|Exercise Comprehension Type|8 Videos

Similar Questions

Explore conceptually related problems

Two variable chords AB and BC of a circle x^(2)+y^(2)=a^(2) are such that AB=BC=a . M and N are the midpoints of AB and BC, respectively, such that the line joining MN intersects the circles at P and Q, where P is closer to AB and O is the center of the circle. The locus of the points of intersection of tangents at A and C is

Two variable chords AB and BC of a circle x^(2)+y^(2)=a^(2) are such that AB=BC=a . M and N are the midpoints of AB and BC, respectively, such that the line joining MN intersects the circles at P and Q, where P is closer to AB and O is the center of the circle. The locus of the points of intersection of tangents at A and C is

A chord AB of circle x^(2) +y^(2) =a^(2) touches the circle x^(2) +y^(2) - 2ax =0 .Locus of the point of intersection of tangens at A and B is :

If the tangents to the parabola y^2=4a x intersect the hyperbola (x^2)/(a^2)-(y^2)/(b^2)=1 at Aa n dB , then find the locus of the point of intersection of the tangents at Aa n dBdot

If there are two points A and B on rectangular hyperbola xy=c^2 such that abscissa of A = ordinate of B, then locusof point of intersection of tangents at A and B is (a) y^2-x^2=2c^2 (b) y^2-x^2=c^2/2 (c) y=x (d) non of these

If a tangent to the parabola y^2 = 4ax intersects the x^2/a^2+y^2/b^2= 1 at A and B , then the locus of the point of intersection of tangents at A and B to the ellipse is

Find the locus of the point of intersection of perpendicular tangents to the circle x^(2) + y^(2)= 4

The tangents PA and PB are drawn from any point P of the circle x^(2)+y^(2)=2a^(2) to the circle x^(2)+y^(2)=a^(2) . The chord of contact AB on extending meets again the first circle at the points A' and B'. The locus of the point of intersection of tangents at A' and B' may be given as

A variable chord of circle x^(2)+y^(2)+2gx+2fy+c=0 passes through the point P(x_(1),y_(1)) . Find the locus of the midpoint of the chord.

The equation of the locus of the middle point of a chord of the circle x^2+y^2=2(x+y) such that the pair of lines joining the origin to the point of intersection of the chord and the circle are equally inclined to the x-axis is x+y=2 (b) x-y=2 2x-y=1 (d) none of these

Home
Profile