The given circle is
`x^(2)+y^(2)=1` (1)
Center `-=O(0,0)` and radius `=1`
Let `T_(1)` and `T_(2)` be the tangents drawn from `(-2,0)` to the circle (1) .

From the figure, `Delta PLO` and `Delta PMC_(1)` are similar. Therefore,
`(OL)/(OP)=(C_(1)M)/(C_(1)P)`
or `(1)/(2)=(r_(1))/(h_(1)+2)`
or `2r_(1)=h_(1)+2` (2)
Also, the circle are touching externally. Therefore,
`h_(1)=r_(1)+1` (3)
From (2) and(3),
`r_(1)=3` and `h_(1)=4`
Hence, `Delta PLO` and `Delta PNC_(2)` are similar. Therefore,
`(OL)/(OP)=(C_(2)N)/(C_(2)P)`
or `(1)/(2)=(r_(2))/(2+h_(2))`
or `2r_(2)=2+h_(2)` (5)
Also, the circles are touching externally. Therefore,
`-h_(2)=1+r_(2)` (6)
From (5) and (6)
`(x+(4)/(3))^(2)+y^(2)=((1)/(3))^(2) ` (7)
Since circles (1) and (4) are two touching circles, they have three common tangents `: T_(1), T_(2),` and `x-1=0`.
Similarly, the common tangents of circles (1) and (7) are `T_(1), T_(2)`, and `x = -1`.
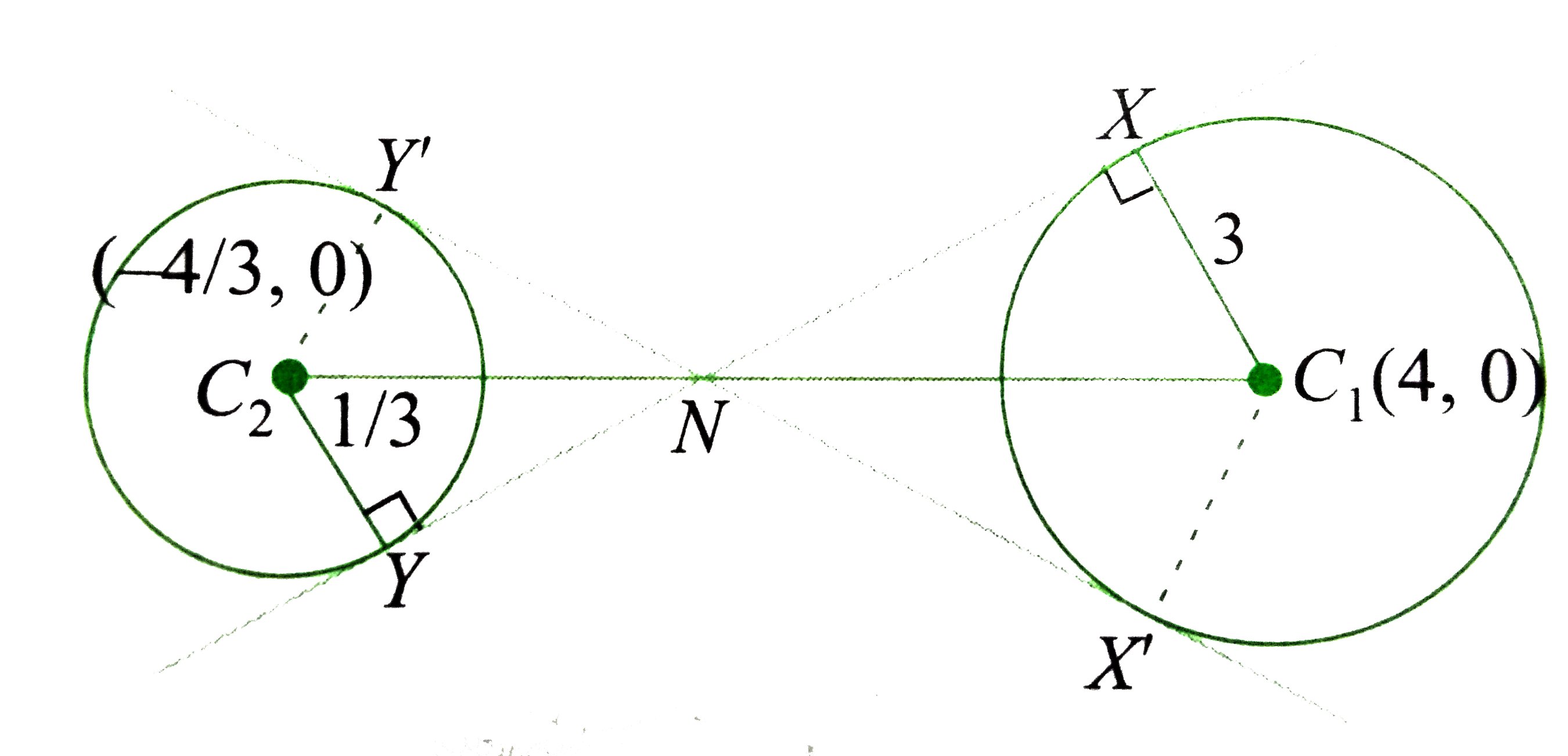
For the circles (4) and (7) , there will be four common tangnets `:` two direct and two indirect.
Two common direct tangents `T_(1)` and `T_(2)`.
Let common direct are `T_(1)` and `T_(2)`
Let us find two common indirect tangents.
`(C_(1)N)/(C_(2)N)=(3)/(1//3)=9`
i.e., N divides `C_(1)C_(2)` in the ratio `9:1`. Therefore,
`N-=((9xx(-4//3)+1xx4)/(10),0)-=((-4)/(5),0)`
Any line through N is
`y=m(x+(4)/(5))`
or `5mx-5y+4m=0`
If it is tangent to circle (4), then
`|(20m+4m)/(sqrt(25m^(2)+25))|=3`
or `24m=15sqrt(m^(2)+1)`
or `64m^(2)=25m^(2)+25`
or `39m^(2)=25m^(2)+25`
or `m= +- (5)/(sqrt(39))`
Therefore, the required tangents are
`y = +- (5)/(sqrt39)(x+(4)/(5))`

