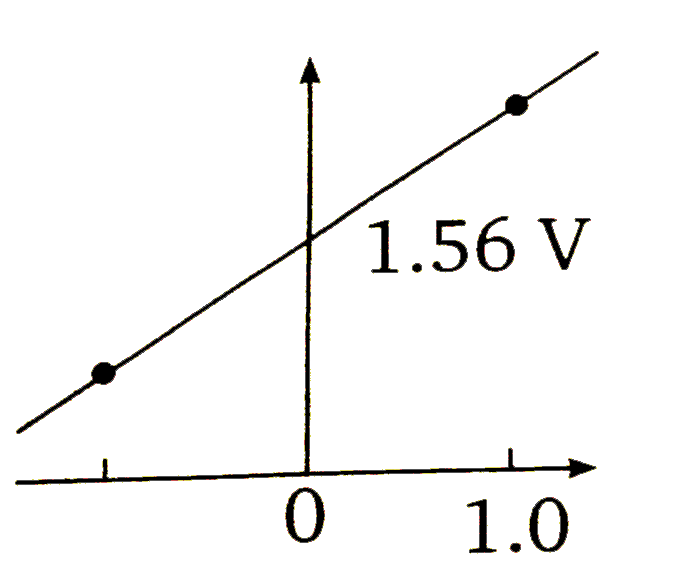
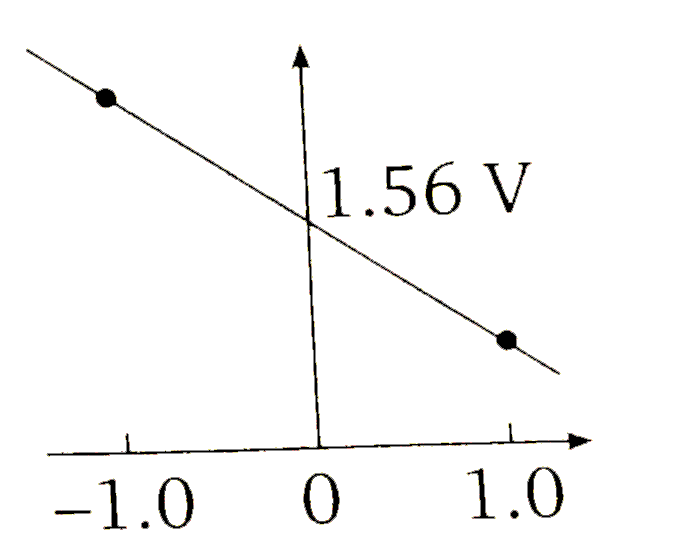
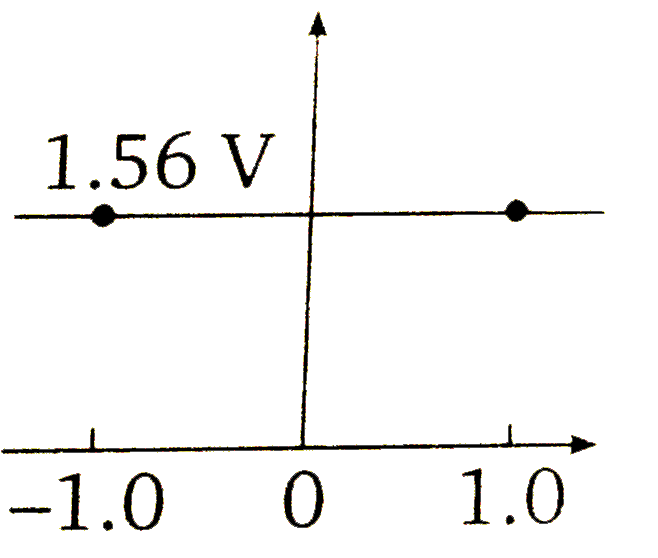A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NARENDRA AWASTHI ENGLISH-ELECTROCHEMISTRY-Subjective problems
- Which graph correctly correlates E(cell) as a function of concentratio...
Text Solution
|
- How many faradays are required for reduction of 1mol C6H5NO2 into C6H5...
Text Solution
|
- What is the equivalent mass of O2 in the following reaction , H2O+1/2O...
Text Solution
|
- The amount of electricity which release 2.0g of gold from a gold salt ...
Text Solution
|
- when molten salt was elctrolysed for 5 min with9.65 A current , 0.18g ...
Text Solution
|
- During the electrolysis of a concentrated brine solution, Calculated t...
Text Solution
|
- Calculate the cell potential (in V) if /\G=-96.5kJ/mol and n=1
Text Solution
|
- If Kc for the reaction Cu^(2+)(aq)+Sn^(2+)(aq)toSn^(4+)(aq)+Cu(s) ...
Text Solution
|
- If /\G^(@) for the half cell MnO4^(-)"|"MnO2 in an acid solution is -x...
Text Solution
|
- If the equilibrium constant for the reaction Cd^(2+)(aq)+4NH3(aq)iffCd...
Text Solution
|
- At What pH oxidation potential of water is -0.81V ?
Text Solution
|
- The resistance of a conductivity cell containing 0.001M KCl solution a...
Text Solution
|
- Molar conductivity at infinitre dilution of KCl,HCl and CH3COOK are 0...
Text Solution
|
- Molar conductivity of aqueous solution of HA is 200Scm^(2)mol^(-1),pH ...
Text Solution
|
- The standard reduction potential of a silver chloride electrode (meta...
Text Solution
|