Home
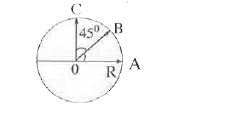
Class 11
PHYSICS
The resultant of the three vectors bar(O...

The resultant of the three vectors `bar(OA), bar(OB) and bar(OC)` has magnitude (R = Radius of the circle)

A

`sqrt2R`

B

`(1 + sqrt2)R`

C

`(sqrt2- 1)R`

D

2R

Text Solution

Verified by Experts

The correct Answer is:
B
Promotional Banner

Topper's Solved these Questions

  • VECTORS

    AAKASH SERIES|Exercise Lecture Sheet (Exercise-I) (Addition of Vectors) (More than correct answer type Questions)|2 Videos

  • VECTORS

    AAKASH SERIES|Exercise Lecture Sheet (Exercise-I) (Integer Type Questions)|3 Videos

  • UNITS AND MEASUREMENTS

    AAKASH SERIES|Exercise ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED))|14 Videos

  • VISCOSITY

    AAKASH SERIES|Exercise Questions for Descriptive Answers|3 Videos

Similar Questions

Explore conceptually related problems

Find the resultant of the vectors vec(OA), vec(OB), vec(OC) as shown in figure. The radius of the circle is r.

Find a vector in the direction of vector bar(a) = bar(i) - 2bar(j) has magnitude 7 units.

The resultant of bar(u) and bar(v) is perpendicular to bar(u) and has a magnitude equal to half of the magnitude of bar(v) . The angle between bar(u) " & " bar(v) is

Find the unit vector in the direction of the sum of the vectors bar(a) = 2bar(i)+ 2bar(j) - 5bar(k) and bar(b) = 2bar(i) + bar(j) + 3bar(k) .

A non-zero vector bar(a) , is parallel to the line of intersection of the plane determined by the vectors bar(i), bar(i) + bar(j) and the plane determined by the vectors bar(i)- bar(j), bar(i) + bar(k) Find the angle between bar(a) and the vector bar(i)- 2bar(j) + 2bar(k)