Text Solution
Verified by Experts
Topper's Solved these Questions
AAKASH SERIES-ELASTICITY-Questions for Descriptive Answers
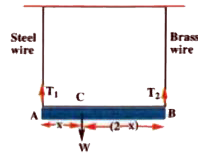
- A light rod of length 2 m is suspended from the ceiling horizontally b...
Text Solution
|
- A steel wire of area of cross-section A and length 2L is clamped firml...
Text Solution
|
- A thin ring of radius R is made of material of density P and young.s m...
Text Solution
|
- A horizontally oriented copper rod of length / is rotating about a ver...
Text Solution
|
- A ring of radius R made of lead wire of breaking strength rho and dens...
Text Solution
|
- A uniform elastic plank moves over a smooth horizontal plane due to a ...
Text Solution
|
- A bar of cross-section A is subjected to equal and opposite tensile fo...
Text Solution
|
- What internal pressure can be sustained by a glass tube of trideness a...
Text Solution
|
- A metallic ring of radius r and cross-sectional area A is fitted into ...
Text Solution
|
- A copper wire 2m long is stretched by Imm. If the energy stored in th...
Text Solution
|
- The work done in stretching a wire by 0.1mm is 4J. Find the work done ...
Text Solution
|