Home
Class 11
PHYSICS
Two bars of masses .m(1). and .m(2). con...

Two bars of masses `.m_(1).` and `.m_(2).` connected by a weightles spring of stiffness constant K as shown in figure, rest on a smooth horizontal plane. Bar 2 is shifted through a small distance x to the left and then released. Find the velocity of the centre of mass of the system after bar 1 breaks off the wall.

Text Solution

Verified by Experts

Velocity of the bar 2 at the instant of break off will be obtained as
`(1)/(2)m_(2)v_(2)^(2)=(1)/(2)kx^(2) " " v_(2)=xsqrt((k)/(m_(2)))`
The velocity of the bar 1 at that instant is zero `(v_(1) = 0)`
The velocity of the centre of mass is give by
`v_(c)=xsqrt((km_(2))/((m_(1)+m_(2))))`
Promotional Banner

Topper's Solved these Questions

  • WORK, POWER & ENERGY

    AAKASH SERIES|Exercise EXERCISE - I|78 Videos

  • WORK, POWER & ENERGY

    AAKASH SERIES|Exercise EXERCISE - II (SCALARS (OR) DOT PRODUCT)|9 Videos

  • WORK POWER ENERGY

    AAKASH SERIES|Exercise EXERCISE - 3|61 Videos

Similar Questions

Explore conceptually related problems

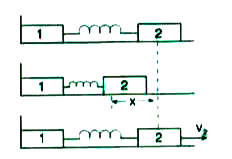
Two bars of masses m, and m, connected by an light spring (intially at its natural length) rests on a horizontal plane. The coefficient of friction between the bars and the surface is mu. The mnimum costant force that bar to be applied in the horizontal direction (along the length of spring) to the bar of mass m_(1) in order to shift the other bar of mass m_(2) Acceleration due to gravity is g) will be

Two blocks m_(1) and m_(2) are connected by a massless spring of force constant k F_(1) and F_(2) are two forces acting on m and m_1 and m_2 as shown. The arrangement is on a horizontal plane.

A particle of mass 'm' attached with one end of a light spring of stiffness (k) is pushed with a speed (v) on a smooth horizontal plane. If l_(0)= natural length of the spring and x_(0) = elongation of the spring at the given instant.