Home
Class 10
MATHS
From a point on a bridge across a river,...

From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are `30^(@) and 45^(@)`, respectively. If the bridge is at a height of 3m from the banks, find the width of the river.

Text Solution

Verified by Experts

The correct Answer is:
`3(sqrt3+1)m`
Promotional Banner

Topper's Solved these Questions

  • SOME AAPLICATIONS OF TRIGONOMETRY

    KUMAR PRAKASHAN|Exercise Other Important Examples|3 Videos

  • SOME AAPLICATIONS OF TRIGONOMETRY

    KUMAR PRAKASHAN|Exercise Exercise9.1|16 Videos

  • REAL NUMBERS

    KUMAR PRAKASHAN|Exercise TEST YOUR SKILLS|26 Videos

  • STATISTICS

    KUMAR PRAKASHAN|Exercise Objective Questions (True or false)|5 Videos

Similar Questions

Explore conceptually related problems

Two poles of equal heights are standing opposite each other on either side of the road, which is 80m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60^(@) and 30^(@) , respectively. Find the height of the poles and the distances of the point from the poles.

Two poles of equal heights are standing opposite to each other on either side of the road, which is 120 feet wide. From a point between them on the road, the angles of elevation of the top of the poles are 60^(@) and 30^(@) respectively. Find the height of the poles and the distances of the point from the poles.

From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20m high building are 45^(@) and 60^(@) respectively. Find the height of the tower.

From the top of a building 60m high, the angles of depression of the top and the bottom of a tower are observed to be 30^(@) and 60^(@) . Find the height of the tower.

A swimmer starts to swim from point a to cross a river. He wants to reach point B on the opposite side of the river. The line AB makes an angle 60^(@) with the river flow as hown. The velocity of the swimmer in still water is same as that of the water (i) In what direction should he try to direct his velocity ? Calculate angle between his velocity anf river velocity. (ii) Find the ratio of the time taken to cross the river in this situation to the minimum time in which he can cross this river.

A swimmer starts to swim from point a to cross a river. He wants to reach point B on the opposite side of the river. The line AB makes an angle 60^(@) with the river flow as shown. The velocity of the swimmer in still water is same as that of the water (i) In what direction should he try to direct his velocity ? Calculate angle between his velocity and river velocity. (ii) Find the ratio of the time taken to cross the river in this situation to the minimum time in which he can cross this river.

As observed from the top of a 75m high lighthouse from the sea-level, the angles of depression of two ships are 30^(@) and 45^(@) . If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships

A bridge across a valley is h metres long. There is a temple in the valley directly below the bridge. The angles of depression of the top of the temple from the two ends of the bridge are alpha and beta . Prove that the height of the bridge above the top of the temple is (h (tan alpha tan beta))/(tan alpha + tan beta) metres.

A window of a house is h metres above the ground. From the window, the angles of elevation and depression of the top and the bottom of another house situated on the opposite sides of the lane are found to be alpha and beta respectively. Prove that the height of the other house is h(1 + tan alpha cot beta) metres.

A boat has to cross a river. It crosses the river by making an angle of 60^(@) with the bank of the river due to the stream of the river and travels a distance of 600m to reach the another side of the river. What is the width of the river?

KUMAR PRAKASHAN-SOME AAPLICATIONS OF TRIGONOMETRY-Objective Questions
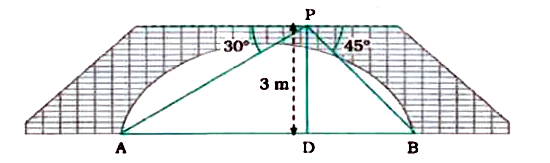
  1. From a point on a bridge across a river, the angles of depression of t...

    Text Solution

    |

  2. A kite is flying at a height of 75m from the level ground, attached to...

    Text Solution

    |

  3. A ladder makes an angle of 60^(@) with the ground, when placed leaning...

    Text Solution

    |

  4. The angle of elevation of the top of a tower from a point on the groun...

    Text Solution

    |

  5. If the height of a man and the length of his shadow are equal, then th...

    Text Solution

    |

  6. The height of a tower is 200m. When the altitude of the Sun is 30^(@),...

    Text Solution

    |

  7. The angle of elevation of the top of a 15m high tower from a point 15m...

    Text Solution

    |

  8. The angle of depression of a boat from a 50m high bridge is 30^(@). Th...

    Text Solution

    |

  9. The angle of elevation of a bird sitting on top of a tree as seen from...

    Text Solution

    |

  10. The length of the shadow of a 10m high tree is ……..m when the angle of...

    Text Solution

    |

  11. The top of two poles of height 16m and 10m are connected by a wire. If...

    Text Solution

    |

  12. The angle of elevation of the top of a tower from a point P on the gro...

    Text Solution

    |

  13. A 1.8m tall girl stands at a distance of 4.6m from a lamp post and cas...

    Text Solution

    |

  14. The angle of elevation of the top of a tower at a distance 500m from t...

    Text Solution

    |

  15. A tower stands on a horizontal plane. The shadow of the tower when the...

    Text Solution

    |

  16. The angle of elevation of the top of a tower from a point 30m away fro...

    Text Solution

    |

  17. The height of a tower is 10m. What is the length of its shadow when th...

    Text Solution

    |

  18. An observer, 1.5m tall, is 28.5m away from a 30m high tower. Determine...

    Text Solution

    |

  19. An observer 1.7m tall, is 20 sqrt3m away from a tower. The angle of el...

    Text Solution

    |

  20. The angle of elevation of the top of an adjustable pole from a point o...

    Text Solution

    |

  21. The two towers of heights x and y, standing on level ground, subtend a...

    Text Solution

    |