Constant force : The magnitude and direction of force acting on the body remains constant during the motion of body , then such type of force is known as constant force .
Definition of work on a trial basis is as under : Work : " The product of magnitude of force and dispalcement during which te force is acts is called work " .
` :. `Work = Force F `xx` Displacement d ...(1)
where F is the force acting on the body and d is the displacement in the direction of force .
Work is denoted by the dot product of force `vec(F)` and displacement in the direction of force .
It is not necessary that the displacement of a body is always in the direction of force of force applied .
If the displacement `vec(d)`
It is not necessary that the displacement of a body is always in the dirction of force applied .
If the displacement of body is not in the direction of force applied then the definition of work is given as under by two ways .
(1) Work = Force `xx` Component of displacement in the direction of force
(2) Work = Component of force in the direction of displacement `xx` displacement ...(3)
Understanding these by following figure (a) a body undergoes a displacement `vec(d)` under the influence of the force `vec(F)` on the body with `theta ` along the horizontal direction .

Force is not fully responsible for displacement `vec(d)` for this take the component of force as shown in figure .
(i) The component of force in the horizontal ( displacement `vec(d)` is not ) direction is `F cos theta `
(ii) Perpendicular component `f sin theta ` to the displacement `vec(d)` is not responsible for horizontal dispalcement .
` :. ` From the equation (3) of definition of work
`W = |vec(F)| cos theta xx |vec(d)|`
` :. W = F cos theta.d`
` [ :. |vec(F)| = F and |vec(d) |=d]`
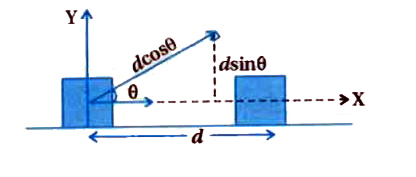
The perpendicular components of displacement `vec(d)` in the direction of force as shown in figure (b) are ,
(1) Component `dcos theta ` in the direction of force `vec(F)`
(2) Component `dsin theta ` in the perpendicular direction of force `vec(F)`
` :. ` From the equation (2) of definition of work ,
`W = |vec(F)| xx|vec(d)| cos theta`
` :. W = F d cos theta " "`...(5)
` [ :. |vec(F ) |= F and |vec(d) | = d.|`
From equation (4) and (5) , the result obtained by two different definition of work is same .
If `theta = 0^(0), cos 0^(0)=1 :. ` Work in general
`W = d cos theta " "....(5)`
` [ :. |vec(F)|=F and |vec(d)| = d]`
From equation (4) and (5) , the result obtained by two different definition of work is same .
If `theta =0^(0) ,cos0^(0)=1 :. ` Work in general
W = Fd which is as equation (1) .
The work obtained by the force acting on the body for definite displacement is proportional to the magnitude of force .

