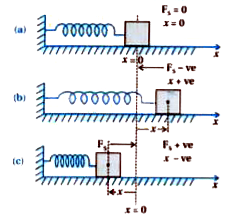
Consider an elastic spring ,obeying Hook.s law with negligible mass whose one end is tied rigidly to a wall as shown in figure . At the other end of the spring a block has been tied and it restring on a smooth horizontal surface .
We shall for the sake of simplicity restrict the motion of the block in the X - direction .
In the normal position of the spring , the position of the block is taken as x=0 ,this is shown as figure (a)
When the block is pulled and the length of spring + x is increased a restoring force `F_(S)` is produced in the spring which tries to bring the spring back to its normal position .the restoring force (spring force ) is produced when the spring is compressed .This is shown in figure (b) and (c) .
The restoring force is directly proportional to the change in the length of the spring and is in the direction opposite to the change in the length . This law of force for the spring is called Hook.s law .
` :. F_(S) = - kx `
where k is the spring constant or force constant of the spring
Spring constant `k = (F_(S))/x` (magnitude ) , its unit is `Nm^(-1)`
The spring is said to be stiff if k is large and soft if it is small .
Suppose that the block is pull outwards as in figure (b) . if the extension is `x_(m)` the work done by the spring force is ,
`W_(S) =int_(0)^(x_(m)) F_(S)dx = - int_(0)^(x_(m)) " "[ :. F_(S)=- kDeltax]`
`=-k[(x^(2))/2]_(0)^(x_(m))`
`=k[(x^(2))/2-0]`
`=-(kx_(m)^(2))/2`
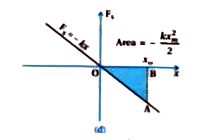
This expression may also be obtained by considereing the area of the triangle as in figure (d). The work done by the external pulling force F is positive since it overcomes the spring force .
If spring is compressed as shown in figure (c) with a displacement `x_(c) ( lt 0)` .The spring force dows work `W_(S) = - (kc_(c)^(2))/2` while the external force F does work + `(kx_(c)^(2))/2`
`W_(S) = - int_(x_(i))^(x_(f))" kx dx" = - k [(x^(2))/2]_(x_(i))^(x_(f))`
`W_(S) =(kx_(i)^(2))/2 - (kx_(f)^(2))/2 `
Hence , the work done by the spring force depends only on the end points .
If the block is pulled from `x_(i)` and allowed to return to`x_(i)` the work done by spring force ,
`W_(S) =-int_(x_(i))^(x_(i))" kx dx" = - k int_(x_(i))^(x_(i)) "x dx" = - k [(x^(2))/2]_(x_(i))^(x_(i))`
` = - k[ (x_(i)^(2))/2-(x_(i)^(2))/2]`
`= 0 `
Hence , the work done by the spring force in a cycle process is zero and so spring force is conservative .