A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
MOTION IN A PLANE
NCERT FINGERTIPS ENGLISH|Exercise Higher Order Thinking Skills|8 VideosMOTION IN A PLANE
NCERT FINGERTIPS ENGLISH|Exercise NCERT Exemplar|10 VideosMOTION IN A PLANE
NCERT FINGERTIPS ENGLISH|Exercise Uniform Circular Motion|14 VideosMECHANICAL PROPERTIES OF SOLIDS
NCERT FINGERTIPS ENGLISH|Exercise Assertion And Reason|15 VideosMOTION IN A STRAIGHT LINE
NCERT FINGERTIPS ENGLISH|Exercise NCERT Exemplar|6 Videos
Similar Questions
Explore conceptually related problems
NCERT FINGERTIPS ENGLISH-MOTION IN A PLANE -Miscellaneous Questions
- vecA and vecB are two vectors. (vecA + vecB) xx (vecA - vecB) can...
Text Solution
|
- If vecA xx vecB = vecC+ vecD, them select the correct alternative:
Text Solution
|
- सिद्ध कीजिए कि |vecA xx vecB|^(2) + |vecA * vecB|^(2) = (AB)^(2).
Text Solution
|
- If vecA and vecB are two vectors, then which of the following is wrong...
Text Solution
|
- If vector A and B have an angle theta between them, then value of |hat...
Text Solution
|
- If the angle between the vectors vecA and vecB is theta, the value of ...
Text Solution
|
- The projection of the vector vecA = hati - 2hatj + hatk on the vector...
Text Solution
|
- The area of the triangle formed by the adjacent sides with vecA = 3hat...
Text Solution
|
- A Body moves 6m north, 8m east and 10m vertically upwards, what is its...
Text Solution
|
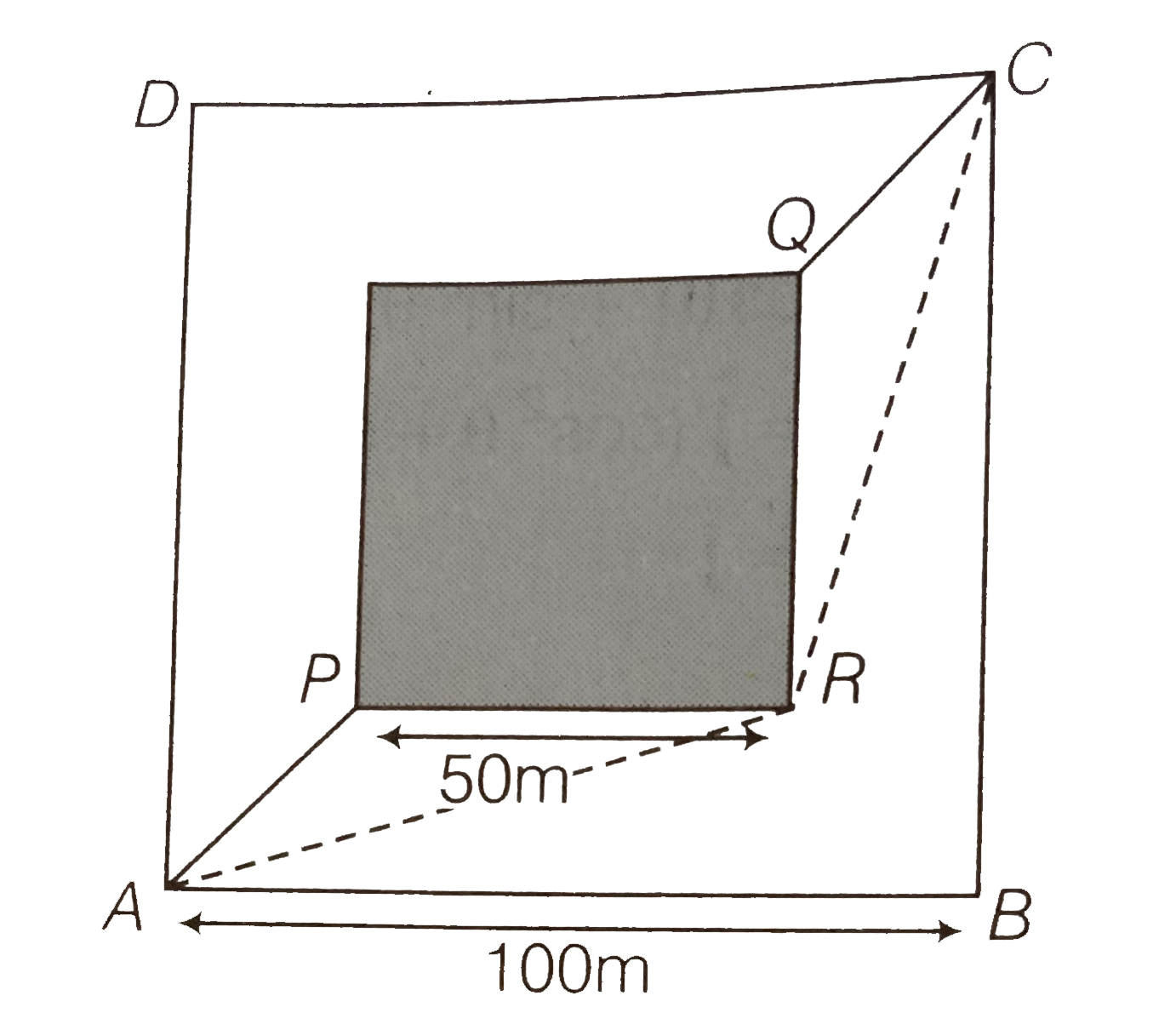
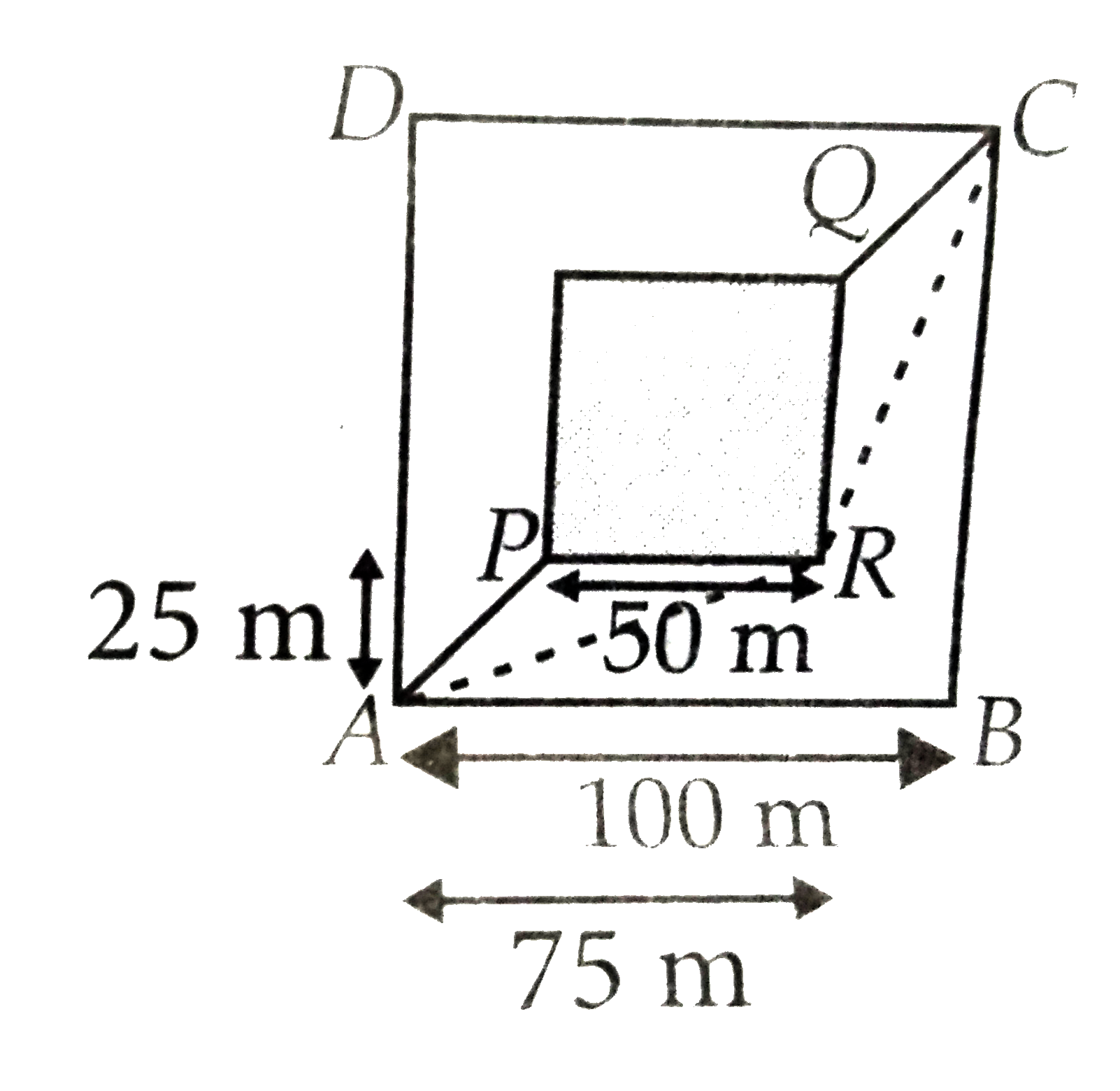
- A man wants to reach from A to the opposite corner of the square C. T...
Text Solution
|
- A man can swim with a speed 4km/hr in still water. (a) How long does...
Text Solution
|
- An aircraft is flying at a height of 3400 m above the ground. If the a...
Text Solution
|
- A fighter plane flying horizontally at an altitude of 1.5 km with spe...
Text Solution
|
- From a building two balls A and B are thrown such that A is thrown up...
Text Solution
|