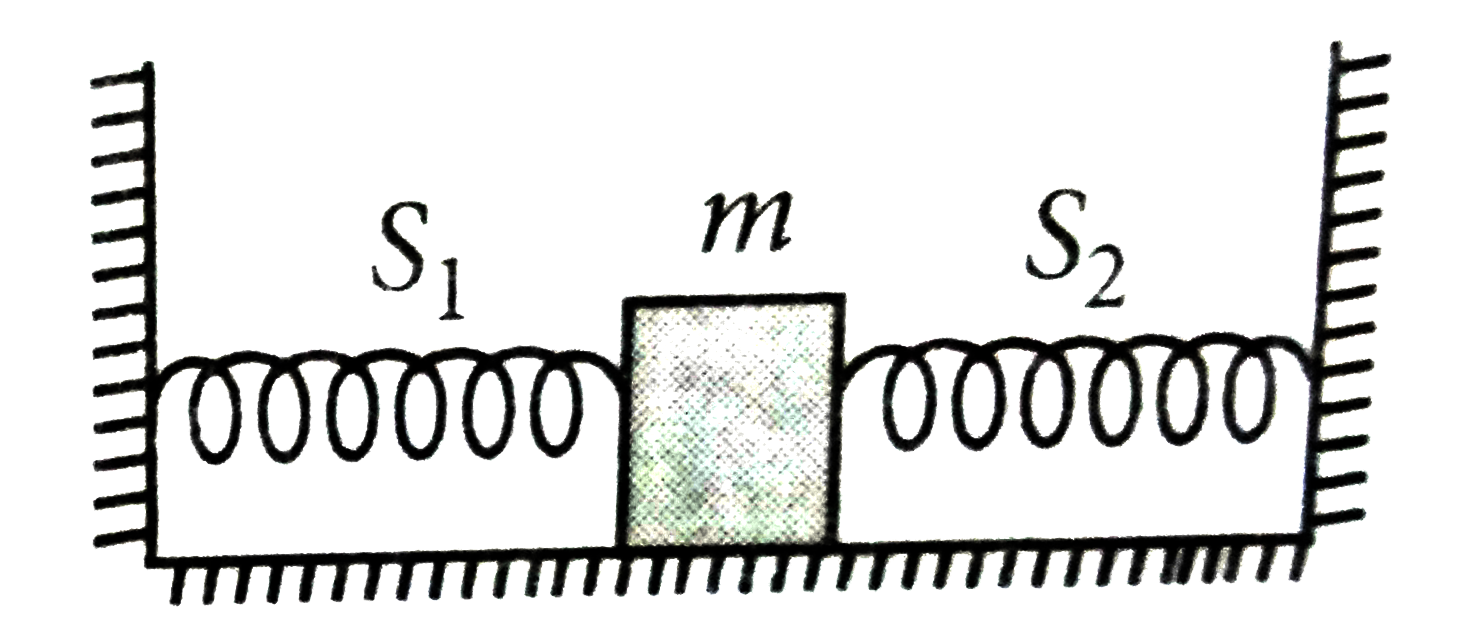A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
OSCILLATIONS
NCERT FINGERTIPS ENGLISH|Exercise Assertion And Reason|15 VideosOSCILLATIONS
NCERT FINGERTIPS ENGLISH|Exercise Forced Oscillation And Resonance|6 VideosMOTION IN A STRAIGHT LINE
NCERT FINGERTIPS ENGLISH|Exercise NCERT Exemplar|6 VideosPHYSICAL WORLD
NCERT FINGERTIPS ENGLISH|Exercise Assertion And Reason|10 Videos
Similar Questions
Explore conceptually related problems
NCERT FINGERTIPS ENGLISH-OSCILLATIONS -NCERT Exemplar
- The displacement of a particle is represented by the equation y=3cos((...
Text Solution
|
- The displacement of a particle is represented by the equation y=sin^(3...
Text Solution
|
- The ralation between acceleration and displacement of four particles a...
Text Solution
|
- Motion of an oscillating liquid column in a U-tube is
Text Solution
|
- A particle is acted simultaneously by mutually perpendicular simple ha...
Text Solution
|
- The displacement of a particle varies with time according to the relat...
Text Solution
|
- Figure shows the circular motion of a particle. The radius of the circ...
Text Solution
|
- The equation of motion of a particle is x=acos(alphat)^(2). The motion...
Text Solution
|
- A particle executing SHM has a maximum speed of 30 cm s^(-1) and a max...
Text Solution
|
- When a mass m is connected individually to two springs S(1) and S2, th...
Text Solution
|