Home
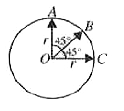
Class 12
PHYSICS
The resultant of the three vectors vec(O...

The resultant of the three vectors `vec(OA), vec(OB)` and `vec(OC)` shown in figure is

A

r

B

2r

C

`r(1+sqrt(s))`

D

`r(sqrt(2)-1)`

Text Solution

Verified by Experts

The correct Answer is:
C
`vec(OC)` and `vec(OA)` are cqual in magnitude and inclined to each other at an angle of `90^(@)`. So their resultant is `sqrt(2r)`. It acts mid-way between `vec(OC)` and `vec(OA)`, ie., along OB. Now, both r and `sqrt(2r)` are along the same line and in the same direction .
Resultant = `r +sqrt(2r) = r (1+sqrt(2))`
Promotional Banner

Topper's Solved these Questions

  • KINEMATICS

    MTG-WBJEE|Exercise WB JEE WORKOUT ( CATEGORY 2 : Single Option Correct Type (2 Marks))|15 Videos

  • KINEMATICS

    MTG-WBJEE|Exercise WB JEE WORKOUT ( CATEGORY 3 : One or More than One Option Correct Type (2 Marks))|10 Videos

  • HEAT AND THERMAL PHYSICS

    MTG-WBJEE|Exercise WB JEE PREVIOUS YEARS QUESTIONS|15 Videos

  • KINETIC THEORY OF GASES

    MTG-WBJEE|Exercise WB JEE PREVIOUS YEARS QUESTIONS (MCQ)|7 Videos

Similar Questions

Explore conceptually related problems

Find the resultant of the three vectors vec(OA), vec(OB) and vec(OC) shown in figure. Radius of the circle is R.

Find the resultant of the three vectors vec OA,vec OB and vec OC each of magnitude r as shown in figure?

What is the angle between the vector vec(A) and vec(B) as shown in figure ?

The magnitude of vectors vec(OA), vec(OB) and vec (OC) in figure are equal. Find the direction of vec(OA)+vec(OB)-vec(OC) . .

The resultant of vectors vec(OA) and vec(OB) is peerpendicular to vec(OA). Find the angle AOB.

The resultant of two vectors vec(P) and vec(Q) is vec(R ) . If the magnitude of vec(Q) is doubled, the new resultant vector becomes perpendicular to vec(P) . Then, the magnitude of vec(R ) is equal to

ABCD is a quadrilateral and E is the point of intersection of the lines joining the middle points of opposite side. Show that the resultant of vec (OA) , vec(OB) , vec(OC) and vec(OD) = 4 vec(OE) , where O is any point.

The resultant of two velocity vectors vec(A) and vec(B) is perpendicular to vec(A) . Magnitude of Resultant vec(R ) is equal to half magnitude of vec(B) . If the angle between vec(A) and vec(B) is (30 theta)^(@) , then value of theta is ?

The resultant of two vectors vec(A) and vec(B) is perpendicular to the vector vec(A) and its magnitudes is equal to half of the magnitudes of vector vec(B) (figure). The angle between vec(A) and vec(B) is

The resultant of two vectors vec(P) and vec(Q) is vec(R) . If vec(Q) is doubled then the new resultant vector is perpendicular to vec(P) . Then magnitude of vec(R) is :-