Home
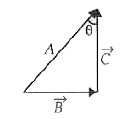
Class 12
PHYSICS
If vecA = vecB + vecC and the magnitude...

If `vecA = vecB + vecC` and the magnitudes of `vecA, vecB and vecC` are 5,4 and 3 units respecetively, the angle between `vecA` and `vecC` is :

A

`cos^(-1) ((3)/(5))`

B

`cos^(-1)((4)/(5))`

C

`(pi)/(2)`

D

`sin^(-1) ((3)/(4))`

Text Solution

Verified by Experts

The correct Answer is:
A
Given : `A=|vecA|=5 , B=|vecB|=4`
`C= |vecC|=3`
As `5^(2)=4^(2)+3^(2)`
`A^(2)=B^(2)+C^(2)`
`:.` Angle between `vecB` and `vecC` is `90^(@)`.
If `theta` is the angle between `vecA` and `vecC` then
`cos theta= (C )/(A) = (3)/(5)`
`theta= cos^(-1) ((3)/(5))`
Promotional Banner

Topper's Solved these Questions

  • KINEMATICS

    MTG-WBJEE|Exercise WB JEE WORKOUT ( CATEGORY 3 : One or More than One Option Correct Type (2 Marks))|10 Videos

  • KINEMATICS

    MTG-WBJEE|Exercise WB JEE Previous Years Questions (CATEGORY 1 : Single Option Correct Type (1 Mark) )|9 Videos

  • KINEMATICS

    MTG-WBJEE|Exercise WB JEE Previous Years Questions (CATEGORY 3 : One or More than One Option Correct Type (2 Marks) )|1 Videos

  • HEAT AND THERMAL PHYSICS

    MTG-WBJEE|Exercise WB JEE PREVIOUS YEARS QUESTIONS|15 Videos

  • KINETIC THEORY OF GASES

    MTG-WBJEE|Exercise WB JEE PREVIOUS YEARS QUESTIONS (MCQ)|7 Videos

Similar Questions

Explore conceptually related problems

The magnitudes of vectors vecA,vecB and vecC are 3,4 and 5 units respectively. If vecA+vecB= vecC , the angle between vecA and vecB is

Given : vecC=vecA+vecB . Also , the magnitude of vecA,vecB and vecC are 12,5 and 13 units respectively . The angle between vecA and vecB is

A magnitude of vector vecA,vecB and vecC are respectively 12, 5 and 13 units and vecA+vecB=vecC then the angle between vecA and vecB is

The magnitudes of vectors vecA.vecB and vecC are respectively 12,5 and 13 unira and vecA+vecB=vecC , then the angle between vecA and vecB is :

Three vectors vecA,vecB and vecC are such that vecA=vecB+vecC and their magnitudes are in ratio 5:4:3 respectively. Find angle between vector vecA and vecC

If veca +vecb +vecc =vec0, |veca| =3 , |vecb|=5 and |vecc| =7 , then the angle between veca and vecb is

vecA, vecB and vecC are vectors such that vecC= vecA + vecB and vecC bot vecA and also C= A . Angle between vecA and vecB is :

If veca,vecb,vecc are unit vectors such that veca is perpendicular to vecb and vecc and |veca+vecb+vecc|=1 then the angle between vecb and vecc is (A) pi/2 (B) pi (C) 0 (D) (2pi)/3

If veca, vecb and vecc are three vectors, such that |veca|=2, |vecb|=3, |vecc|=4, veca. vecc=0, veca. vecb=0 and the angle between vecb and vecc is (pi)/(3) , then the value of |veca xx (2vecb - 3 vecc)| is equal to