Home
Class 12
MATHS
Determine the maximum value of z = 3x + ...

Determine the maximum value of z = 3x + 4y if the feasible region (shaded) for a LPP is shown in Figure.

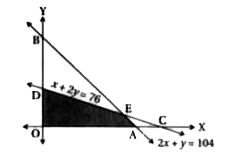
Text Solution

Verified by Experts

The correct Answer is:
Maximum value of objective function z = 3x + 4y is 196 for point (44, 16)
Promotional Banner

Topper's Solved these Questions

  • LINEAR PROGRAMMING

    KUMAR PRAKASHAN|Exercise MULTIPLE CHOICE QUESTIONS|42 Videos

  • LINEAR PROGRAMMING

    KUMAR PRAKASHAN|Exercise PRACTICE PAPER - 12|14 Videos

  • LINEAR PROGRAMMING

    KUMAR PRAKASHAN|Exercise TEXTBOOK ILLUSTRATIONS FOR PRACTICE WORK|11 Videos

  • INVERSE TRIGONOMETRIC FUNCTIONS

    KUMAR PRAKASHAN|Exercise PRACTICE PAPER - 2 (SECTION - D)|2 Videos

  • MATRICES

    KUMAR PRAKASHAN|Exercise Practice Paper - 3 (Section - D)|1 Videos

Similar Questions

Explore conceptually related problems

Feasible region (shaded) for a LPP is shown in Figure Maximise z = 5x + 7y.

In Figure, the feasible region (shaded) for a LPP is shown. Determine the maximum and minimum value of z = x + 2y.

The feasible region for a LPP is shown in Figure. Find the minimum value of z=11x+7y .

In a LPP if the objective function z = ax + by has the same maximum value on two corner points of the feasible region, then every point on the line segment joining these two points give the same ………. Value.

Determine the maximum value of z = 11x + 7y subject to the constraints : 2x+y le 6, x le 2, x ge 0, y ge 0

Find the maximum value of Z = x + y, subject to the constraints x-y le -1, -x+y le 0, x, y ge 0 .

If |z+4|le3 then the maximum value fo |z+1| is....

Find the maximum value of Z = 4x + y subject to the constraints 2x+y le 23, x ge 0, y ge 0 is ……….

The maximum value of Z = 3x + 4y subject to constraints x + y le 4, x ge 0, y ge 0 is _________

The maximum value of Z = x + 4y subject to the constraints 3x+6y le 6, 4x+8y ge 16, x ge 0, y ge 0 is ………

KUMAR PRAKASHAN-LINEAR PROGRAMMING-SOLUTIONS OF NCERT EXEMPLAR PROBLEMS
  1. Maximize the function z = 11x + 7y , subject to the constraints : x le...

    Text Solution

    |

  2. Minimise z = 13x - 15y subject to the constraints : x+y le 7, 2x-3y+6...

    Text Solution

    |

  3. Determine the maximum value of z = 3x + 4y if the feasible region (sha...

    Text Solution

    |

  4. Feasible region (shaded) for a LPP is shown in Figure Maximise z = 5x ...

    Text Solution

    |

  5. The feasible region for a LPP is shown in Figure. Find the minimum val...

    Text Solution

    |

  6. Find the maximum value of Z = 4x + y subject to the constraints 2x+y l...

    Text Solution

    |

  7. The feasible region for a LPP is shown in Figure. Evaluate z = 4x + y ...

    Text Solution

    |

  8. In Figure, the feasible region (shaded) for a LPP is shown. Determine ...

    Text Solution

    |

  9. A manufacturer of electronic circuits has a stock of 200 resistors, 12...

    Text Solution

    |

  10. A firm has to transport 1200 packages using large vans which can carry...

    Text Solution

    |

  11. A company manufactures two types of screws A and B. All the screws hav...

    Text Solution

    |

  12. A man rides his motorcycle at the speed of 50 km/hour. He has to spen...

    Text Solution

    |

  13. Refer to question 11. How many of circuits of Type A and of Type B, sh...

    Text Solution

    |

  14. Find the minimum value of Z = x + y subject to the constraints 2x+3y l...

    Text Solution

    |

  15. Solve the following linear programming problems graphically : Maximi...

    Text Solution

    |

  16. Solve the following linear programming problems graphically : Maximi...

    Text Solution

    |

  17. Refer to question 15. Determine the maximum distance that the man can ...

    Text Solution

    |

  18. Maximise z = x + y subject ot x+4y le 8, 2x+3y le 12, 3x+y le 9, x ge ...

    Text Solution

    |

  19. A manufacturer produces two models of bikes model X and model Y. Model...

    Text Solution

    |

  20. In order to supplement daily diet, a person wishes to take some of x a...

    Text Solution

    |