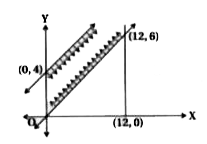
The feasible region for an LLP is shown ...

The feasible region for an LLP is shown in the Figure. Let z = 3x - 4y be the objective function. Maximum value of z is

A

0

B

8

C

12

D

-18

Text Solution

Verified by Experts

The correct Answer is:

C

Topper's Solved these Questions

LINEAR PROGRAMMING
KUMAR PRAKASHAN|Exercise MULTIPLE CHOICE QUESTIONS|42 Videos
LINEAR PROGRAMMING
KUMAR PRAKASHAN|Exercise PRACTICE PAPER - 12|14 Videos
LINEAR PROGRAMMING
KUMAR PRAKASHAN|Exercise TEXTBOOK ILLUSTRATIONS FOR PRACTICE WORK|11 Videos
INVERSE TRIGONOMETRIC FUNCTIONS
KUMAR PRAKASHAN|Exercise PRACTICE PAPER - 2 (SECTION - D)|2 Videos
MATRICES
KUMAR PRAKASHAN|Exercise Practice Paper - 3 (Section - D)|1 Videos

Similar Questions

Explore conceptually related problems

The feasible region for an LLP is shown in the Figure. Let z = 3x - 4y be the objective function. Minimum value of z is

The feasible solution for a LPP is shown in Figure Let z = -3x - 4y objective function. Maximum of Z occurs at

The feasible solution for a LPP is shown in Figure Let z = -3x - 4y objective function. Minimum of Z occurs at

Feasible region (shaded) for a LPP is shown in Figure Maximise z = 5x + 7y.

The feasible region for a LPP is shown in Figure. Evaluate z = 4x + y at each of the corner points at this region. Find the minimum value of z, if exists.

The feasible region for a LPP is shown in Figure. Find the minimum value of z=11x+7y .

If the feasible region for a LPP is …………, then the optimal value of the objective function z = ax + by may or may not exist.

Corner points of the feasible region for an LPP are (0, 2), (3, 0), (6, 0), (6, 8) and (0, 5). Let F = 4x + 6y be the objective function. (Maximum of F)-(Minimum of F) =

Corner points of the feasible region for an LPP are (0, 2), (3, 0), (6, 0), (6, 8) and (0, 5). Let F = 4x + 6y be the objective function. The Minimum value of F occurs at ………..

If the feasible region for a LPP is unbounded, maximum or minimum of the objective function Z = ax + by may or may not exist.

KUMAR PRAKASHAN-LINEAR PROGRAMMING-SOLUTIONS OF NCERT EXEMPLAR PROBLEMS

The corner points of the feasible region determined by the system of l...
Text Solution
|
The feasible solution for a LPP is shown in Figure Let z = -3x - 4y ...
Text Solution
|
The feasible solution for a LPP is shown in Figure Let z = -3x - 4y ...
Text Solution
|
The corner points of the bounded feasible region are (0, 0), (0, 8), (...
Text Solution
|
The feasible region for an LLP is shown in the Figure. Let z = 3x - 4y...
Text Solution
|
The feasible region for an LLP is shown in the Figure. Let z = 3x - 4y...
Text Solution
|
Corner points of the feasible region for an LPP are (0, 2), (3, 0), (6...
Text Solution
|
Corner points of the feasible region for an LPP are (0, 2), (3, 0), (6...
Text Solution
|
Corner points of the feasible region determined by the system of linea...
Text Solution
|
In a LPP, the linear inequalities or restrictions on the variables are...
Text Solution
|
In a LPP, the objective function is always ………….
Text Solution
|
If the feasible region for a LPP is …………, then the optimal value of th...
Text Solution
|
In a LPP if the objective function z = ax + by has the same maximum va...
Text Solution
|
A feasible region of a system of linear inequalities is said to be ………...
Text Solution
|
A corner point of a feasible region is a point in the region which is ...
Text Solution
|
The feasible region for an LLP is always a …….. polygon.
Text Solution
|
If the feasible region for a LPP is unbounded, maximum or minimum of t...
Text Solution
|
Maximum value of the objective function Z = ax + by in a LPP always oc...
Text Solution
|
In a LPP, the minimum value of the objective function Z = ax + by is a...
Text Solution
|
In a LPP, the maximum value of the objective function z = ax + by is a...
Text Solution
|