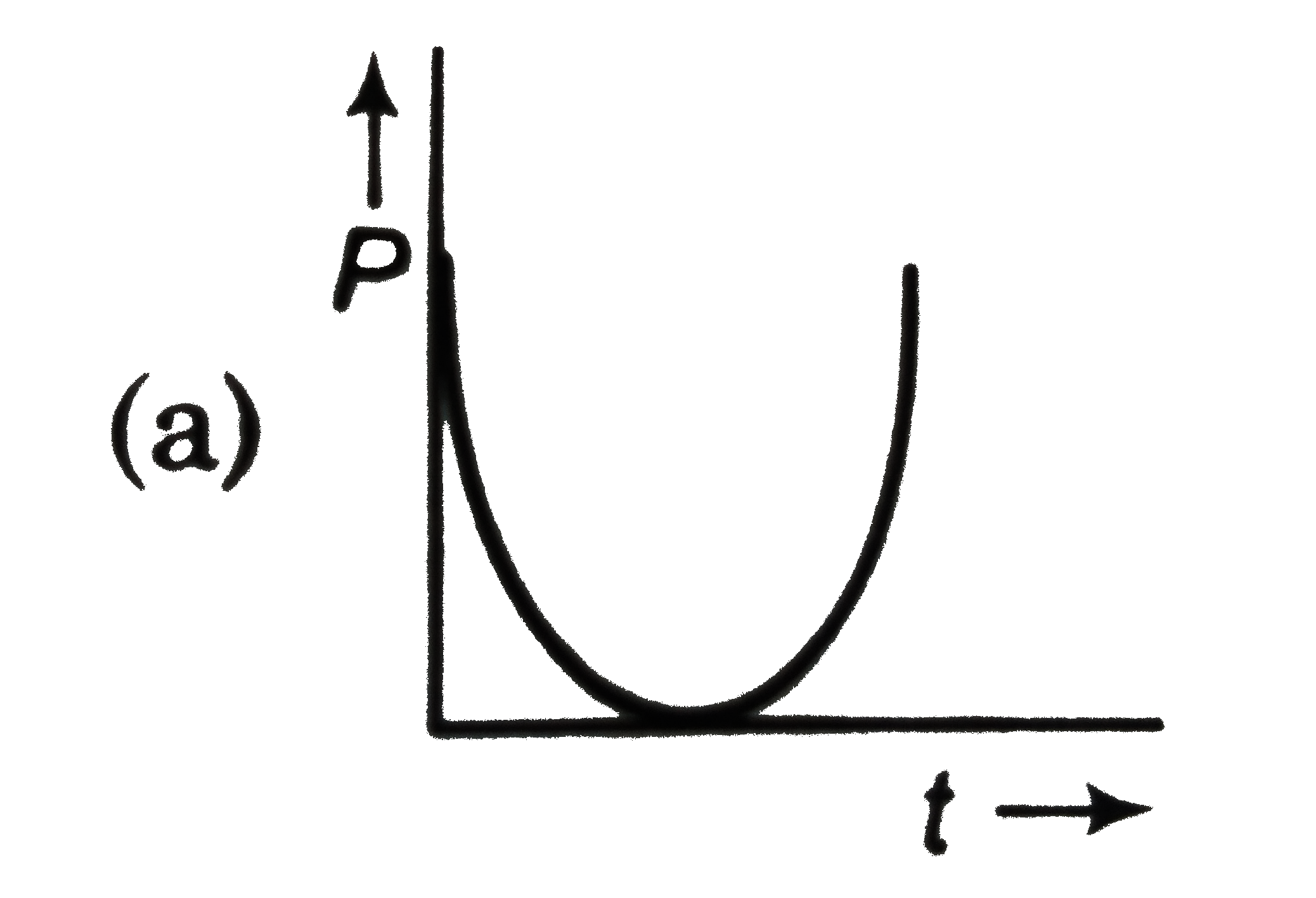
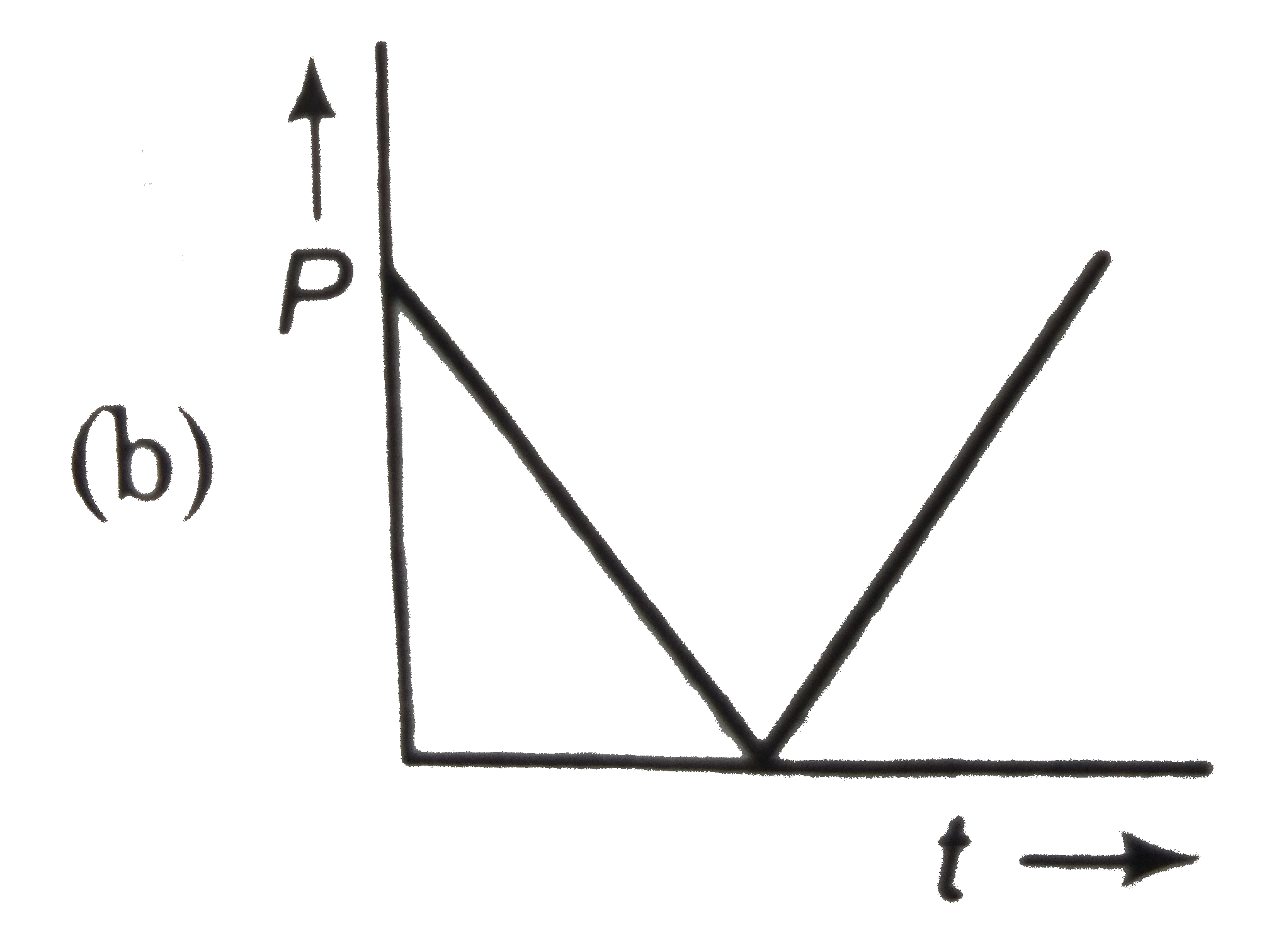
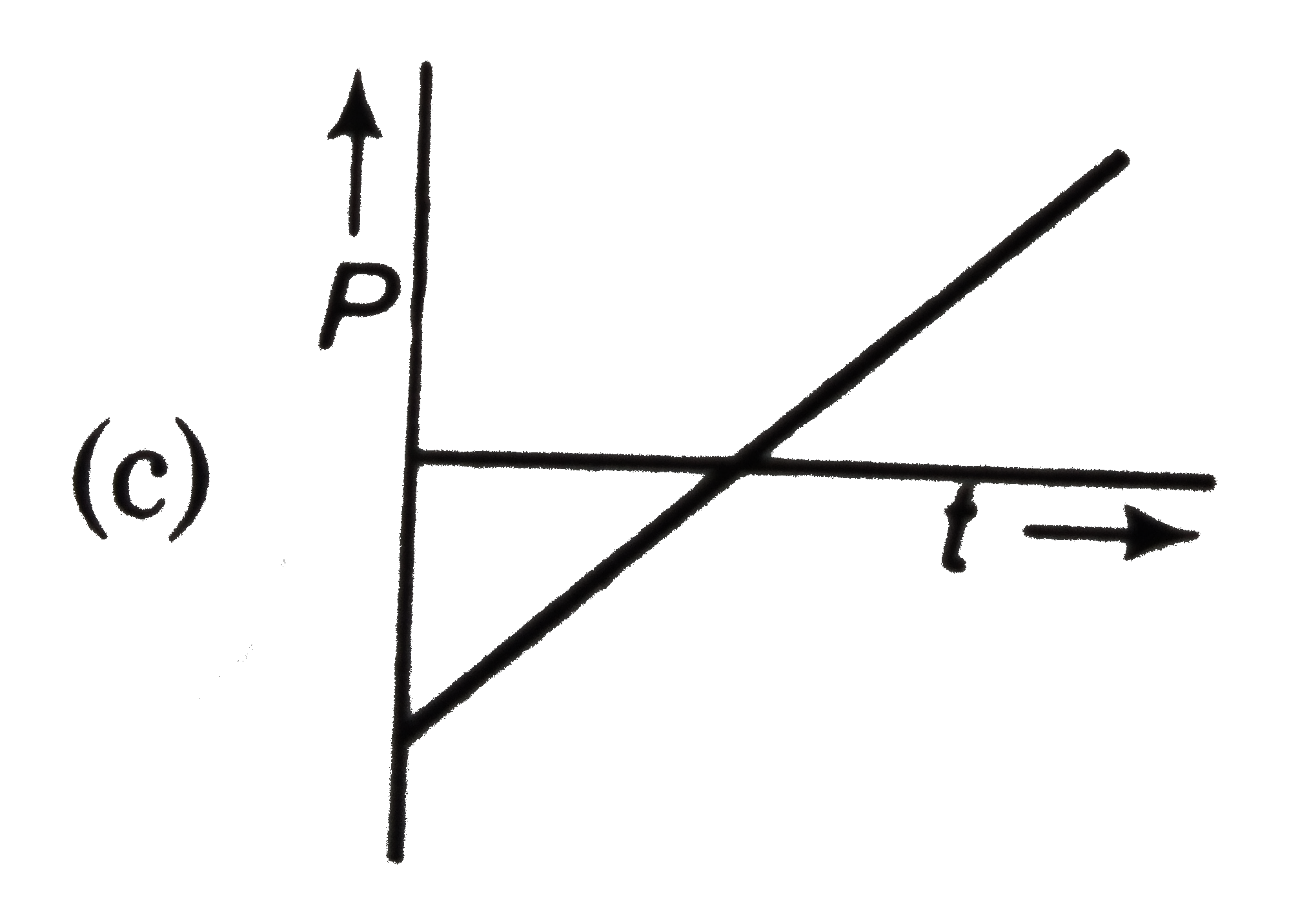
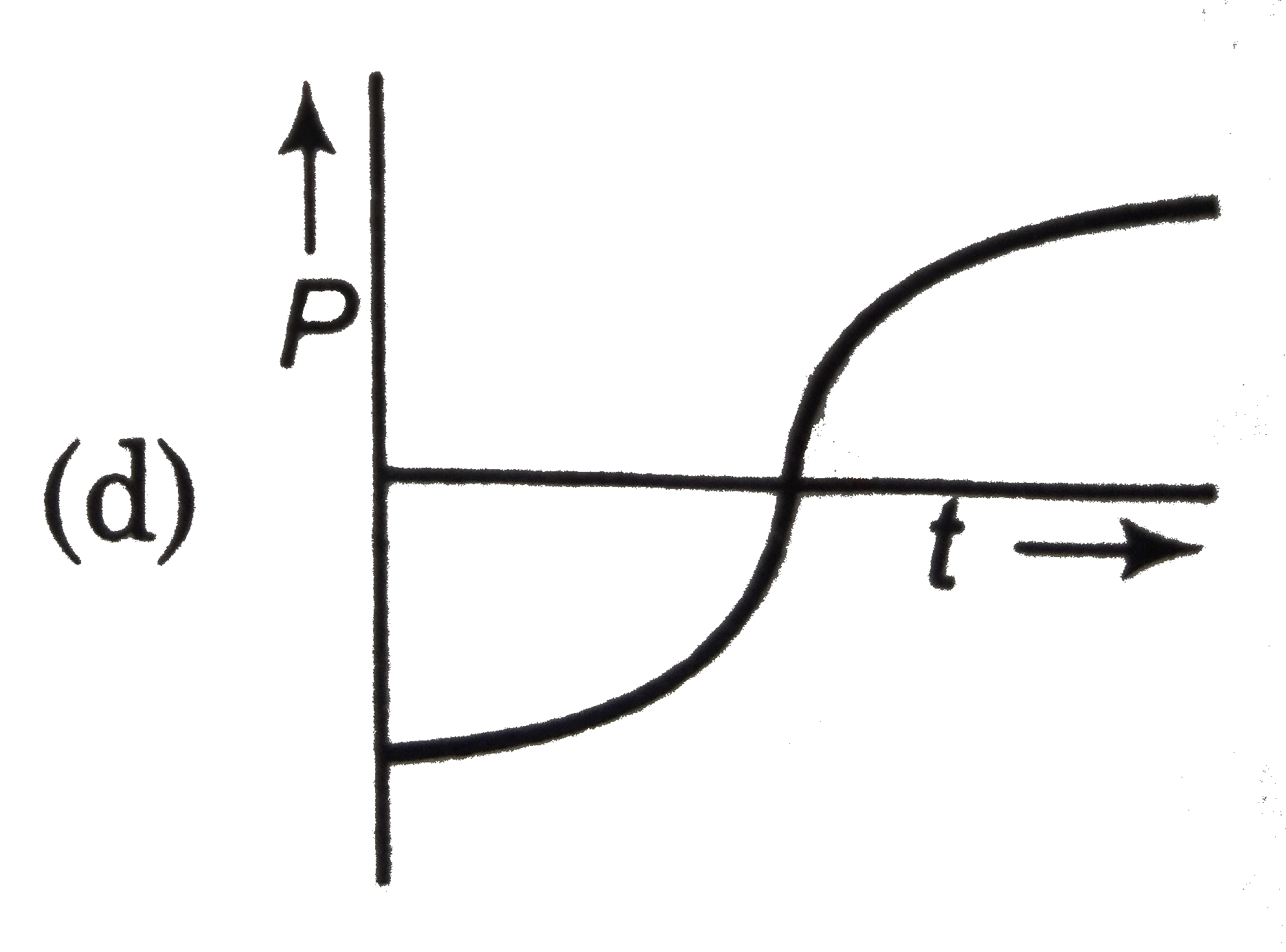
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
WORK, ENERGY & POWER
DC PANDEY ENGLISH|Exercise Level 2 More Than One Correct|9 VideosWORK, ENERGY & POWER
DC PANDEY ENGLISH|Exercise Level 2 Subjective|15 VideosWORK, ENERGY & POWER
DC PANDEY ENGLISH|Exercise Level 1 subjective|27 VideosWAVE MOTION
DC PANDEY ENGLISH|Exercise Integer Type Question|11 VideosWORK, ENERGY AND POWER
DC PANDEY ENGLISH|Exercise MEDICAL ENTRACES GALLERY|33 Videos
DC PANDEY ENGLISH-WORK, ENERGY & POWER-Level 2 Objective
- A body is moving is down an inclined plane of slope 37^@ the coefficie...
Text Solution
|
- The given plot shows the variation of U, the potential energy of inter...
Text Solution
|
- A particle is projected at t=0 from a point on the ground with certain...
Text Solution
|
- A block of mass m is attached to one end of a mass less spring of spri...
Text Solution
|
- A block of mass (m) slides along the track with kinetic friction mu. A...
Text Solution
|
- The potential energy phi in joule of a particle of mass 1 kg moving in...
Text Solution
|
- The force acting on a body moving along x-axis variation of the partic...
Text Solution
|
- A small mass slides down an inclined plane of inclination theta with t...
Text Solution
|
- Two light vertical springs with equal natural length and spring consta...
Text Solution
|
- A block of mass 1kg slides down a curved track which forms one quadran...
Text Solution
|
- The potential energy function for a diatomic molecule is U(x) =(a)/(x^...
Text Solution
|
- A rod mass (M) hinged at (O) is kept in equilibrium with a spring of s...
Text Solution
|
- In the figure. (m2) (< m(1)) are joined together by a pulley. When the...
Text Solution
|
- A particle free to move along x-axis is acted upon by a force F=-ax+b...
Text Solution
|
- Equal net forces act on two different block (A) and (B) masses (m) and...
Text Solution
|
- The potential energy function of a particle in the x-y plane is given ...
Text Solution
|
- A vertical spring is fixed to one of its end and a massless plank plan...
Text Solution
|
- A uniform chain of length of length pir lies inside a smooth semicircu...
Text Solution
|
- A block of mass m is connected to a spring of force constant k. Initia...
Text Solution
|
- Two blocks are connected to an ideal spring of stiffness 200 N//m. At ...
Text Solution
|