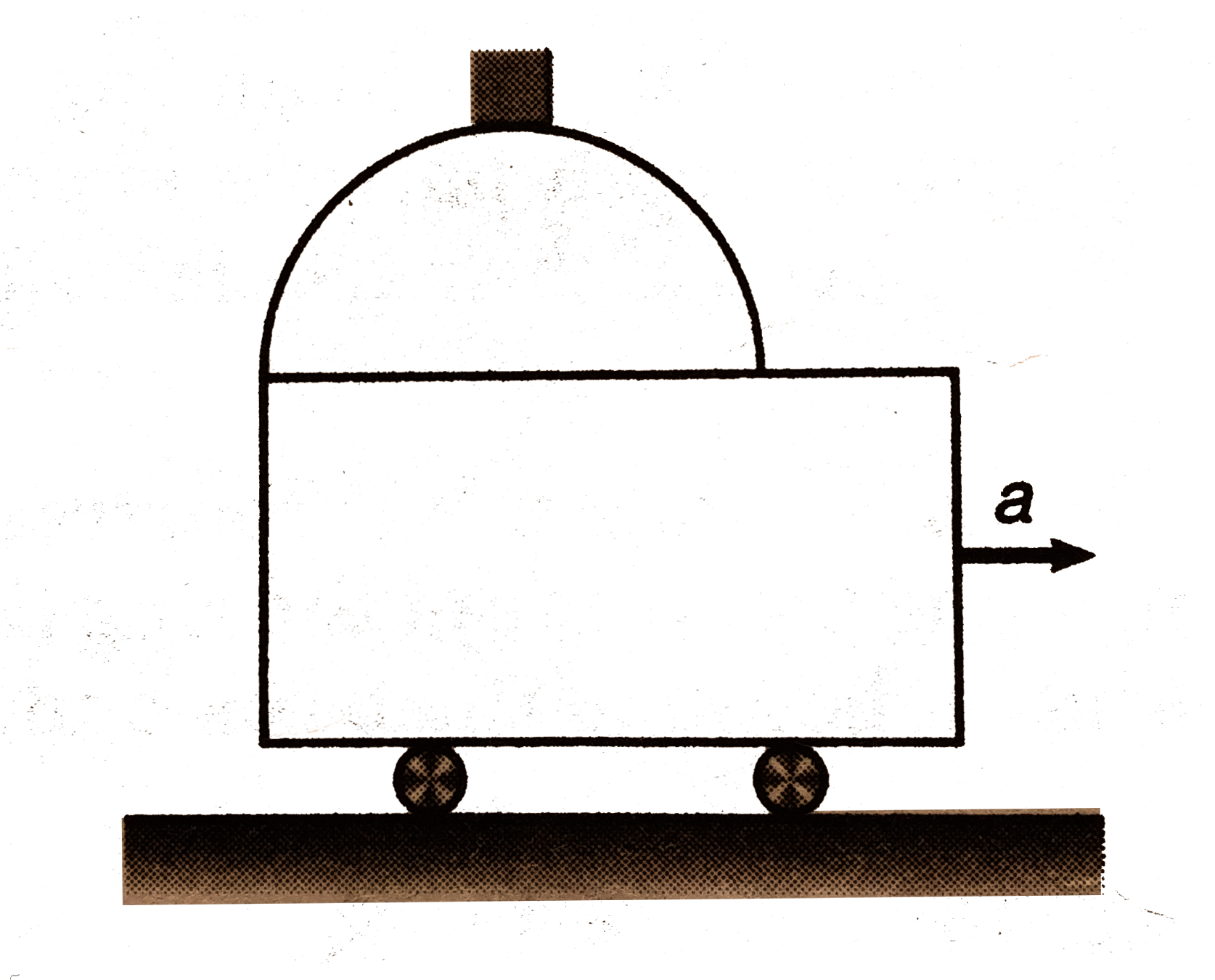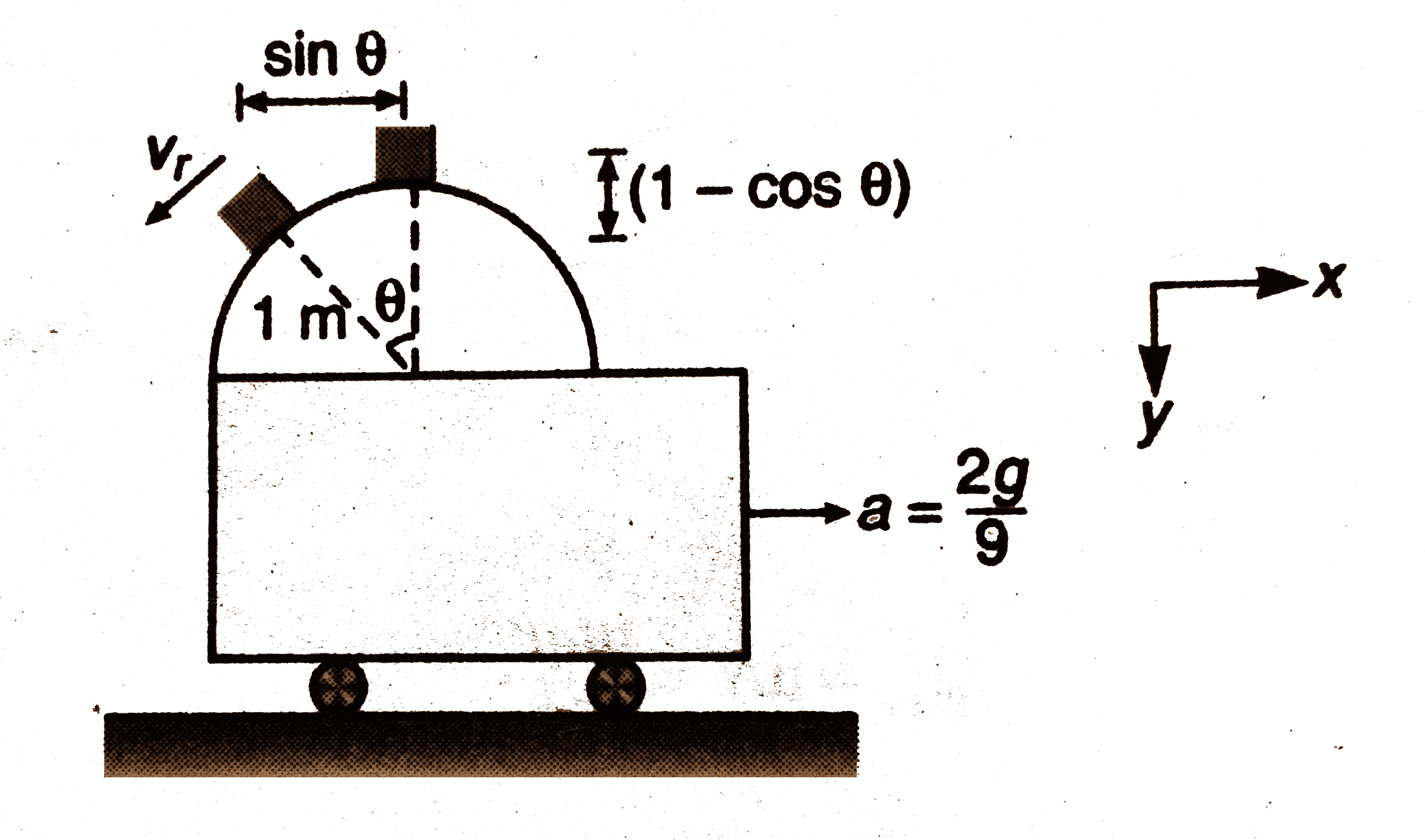Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
CIRCULAR MOTION
DC PANDEY ENGLISH|Exercise JEE Main|23 VideosCIRCULAR MOTION
DC PANDEY ENGLISH|Exercise JEE Advanced|24 VideosCIRCULAR MOTION
DC PANDEY ENGLISH|Exercise Level 2 Subjective|13 VideosCENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
DC PANDEY ENGLISH|Exercise Level 2 Subjective|21 VideosCOMMUNICATION SYSTEM
DC PANDEY ENGLISH|Exercise Only One Option is Correct|27 Videos
Similar Questions
Explore conceptually related problems