`omega=2t^(2)impliesalpha=(domega)/(dt)=4t`
at `t=1s`, `omega=2rad//s` and `alpha=4rad//s^(2)`
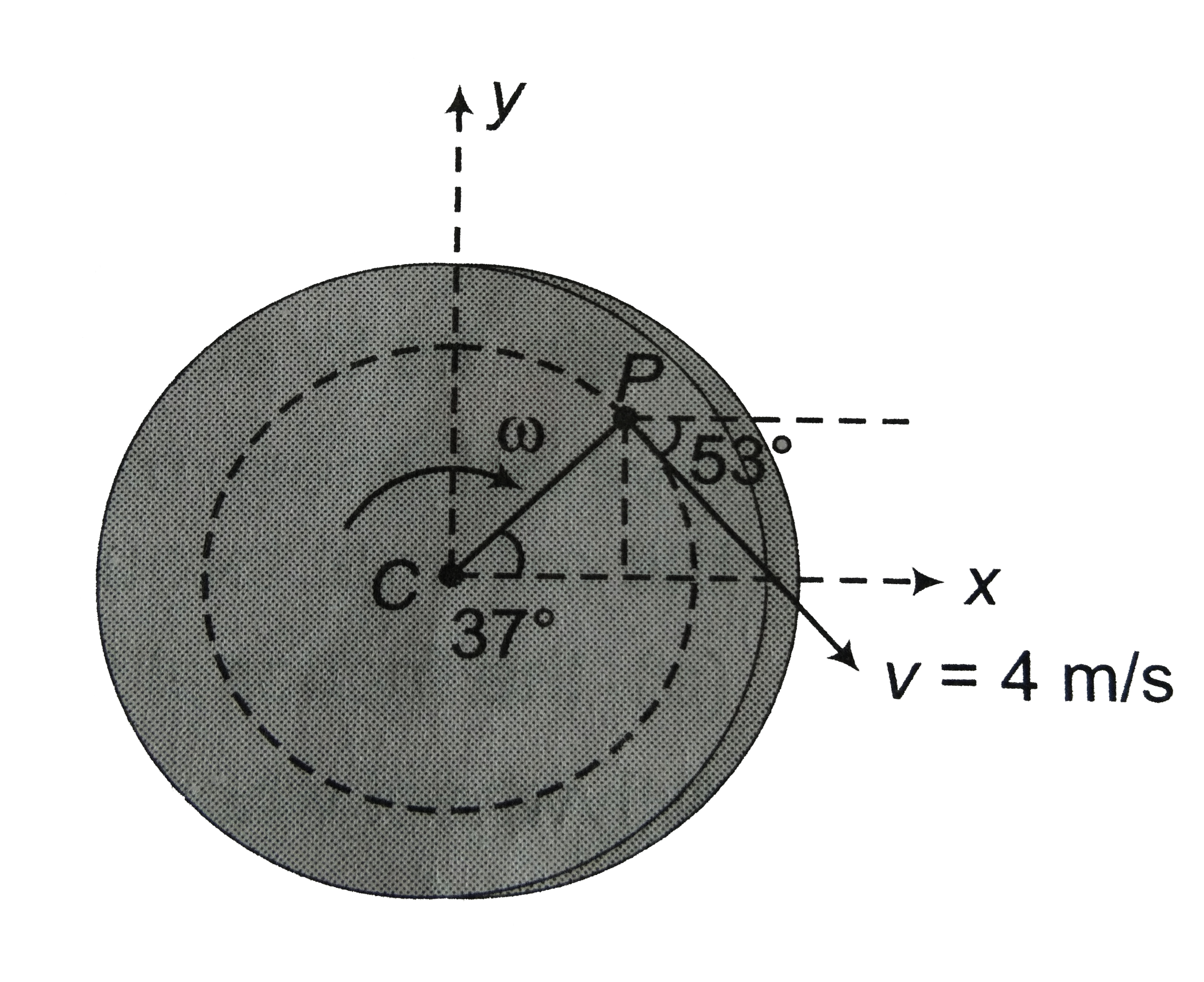
for the particle at `P`, `r=CP=2m`
(a). Rotation is clockwise. So according to right hand rule `omega` is perpendicular to paper inwards along negative z-direction
`thereforeomega=(-2hatk)rad//s`
(b). `omega` is increasing. so `alpha` is alos in the direction of `omega`
`thereforealpha=(-4hatk)rad//s^(2)`
(c). `v=romega=(2)(2)=4m//s`
This velocity is tangential to the doted circle of `P` as shown in figure. `thereforev=(4cos53^(@))hati-(4sin53^(@))hatj`
or `v=(2.4hati-3.2hatj)m//s`
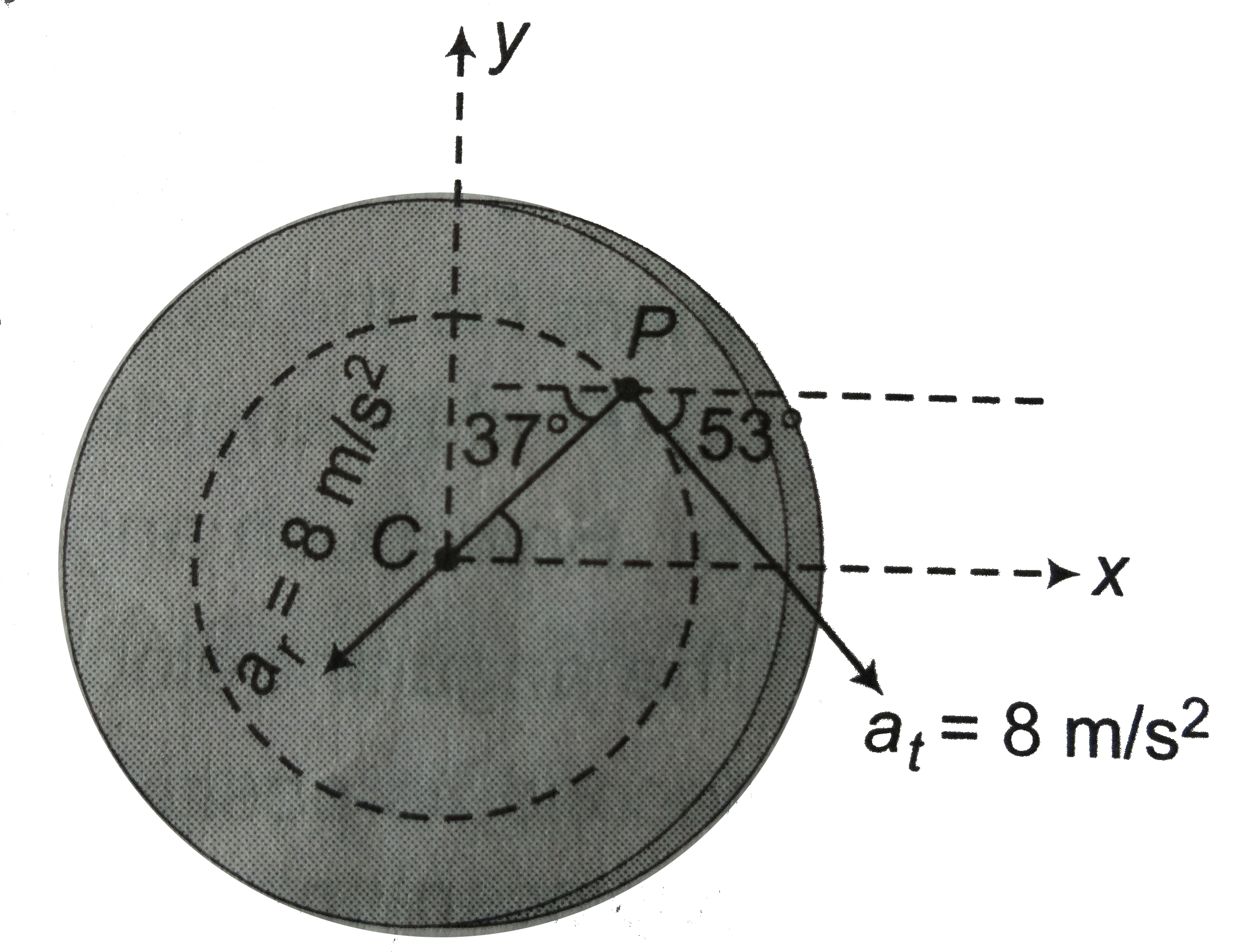
(d). Acceleration of the particle has two components
(i). `a_(r)=romega^(2)` (radial component)
`=(2)(2)^(2)=8m//s^(2)`
this components is towareds centre C.
(ii). `a_(t)=ralpha` (tangential component)
`=(2)(4)=8m//s^(2)`
this component is in the direction of linear velocity, as `omega` or `v` is increasing
`thereforea=(8cos53^(@)-8cos37^(@))(hati)`
`+(8sin53^(@)+8sin37^(@))(-hatj)`
or `a=(-1.6hati-11.2hatj)m//s^(2)`