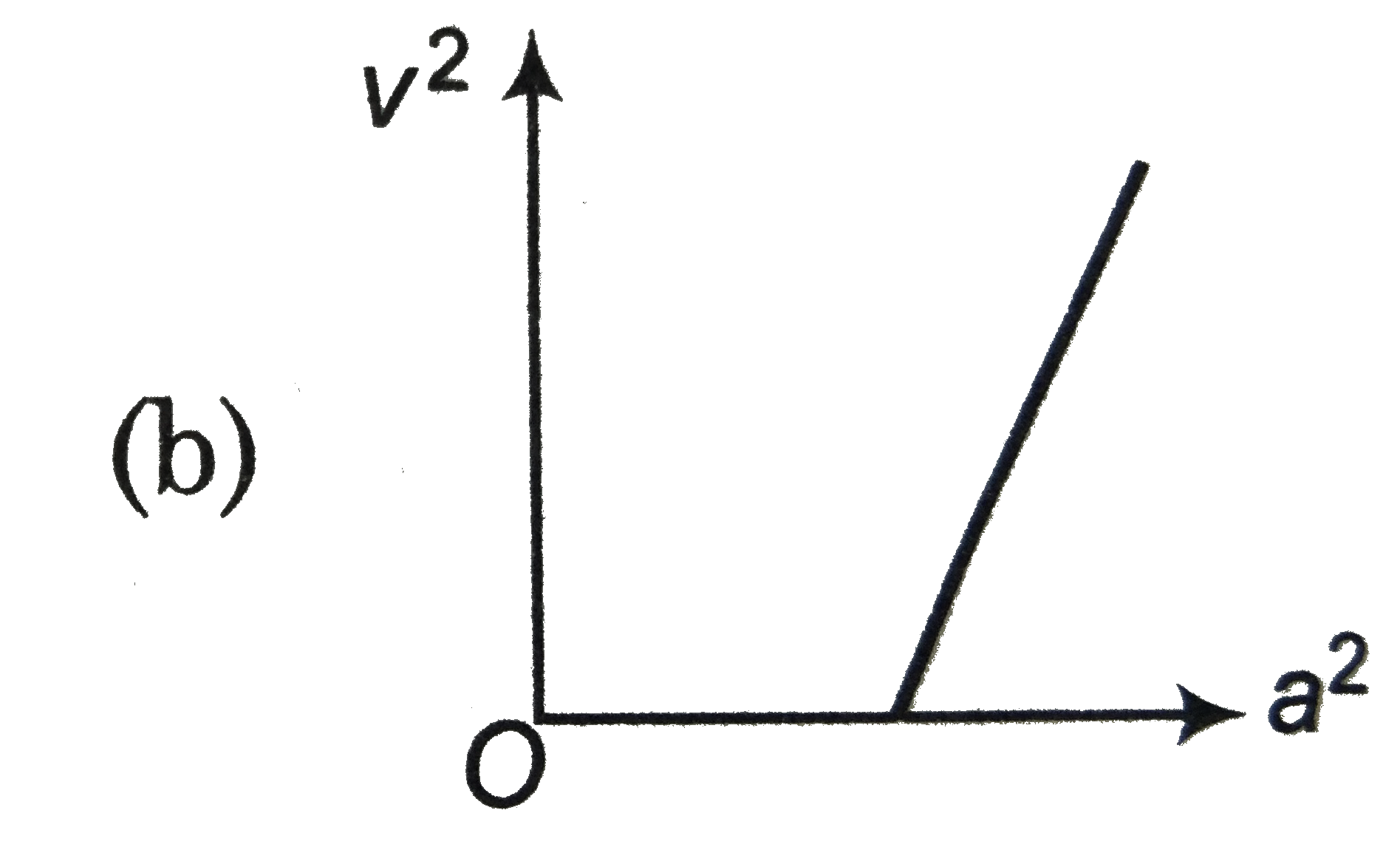
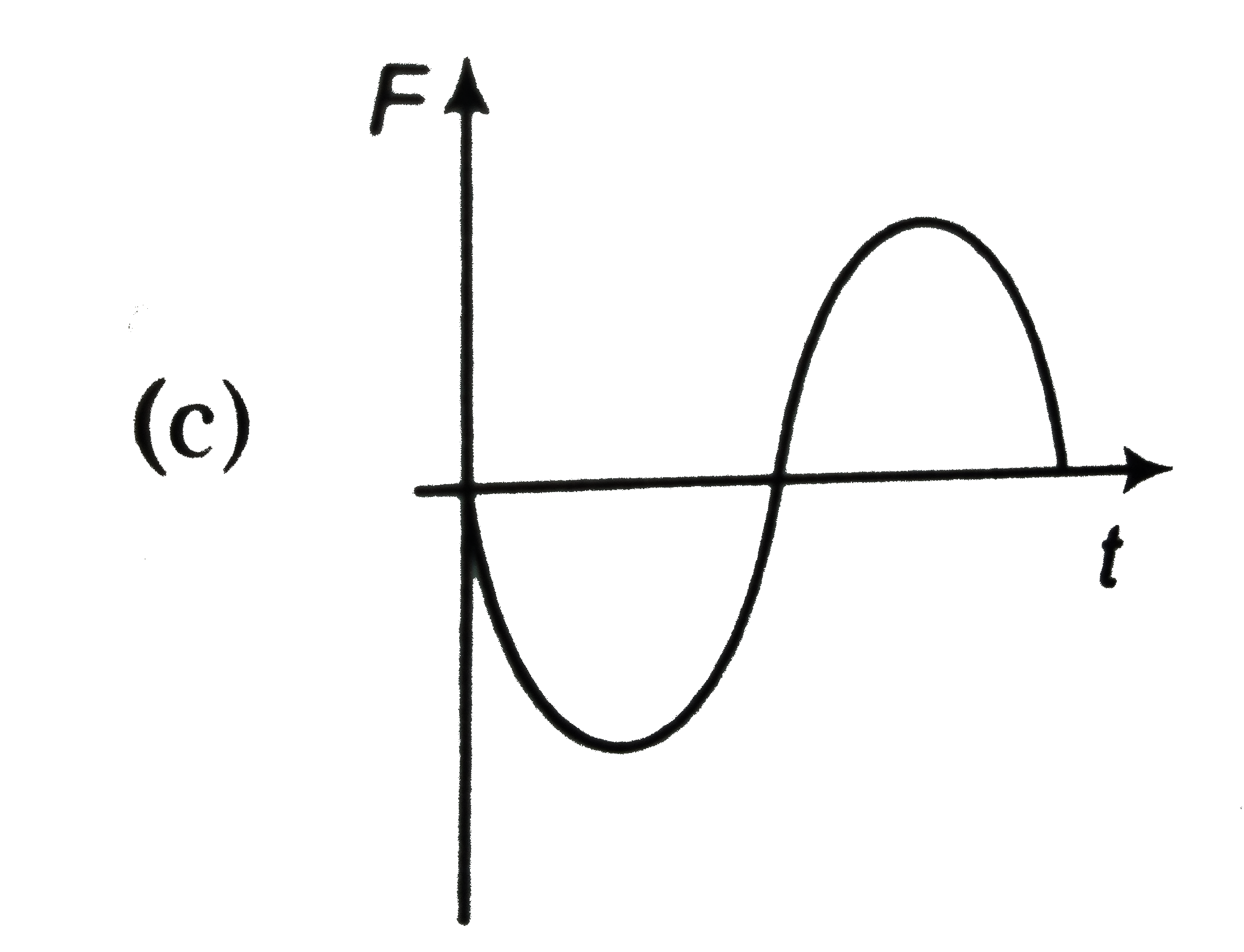
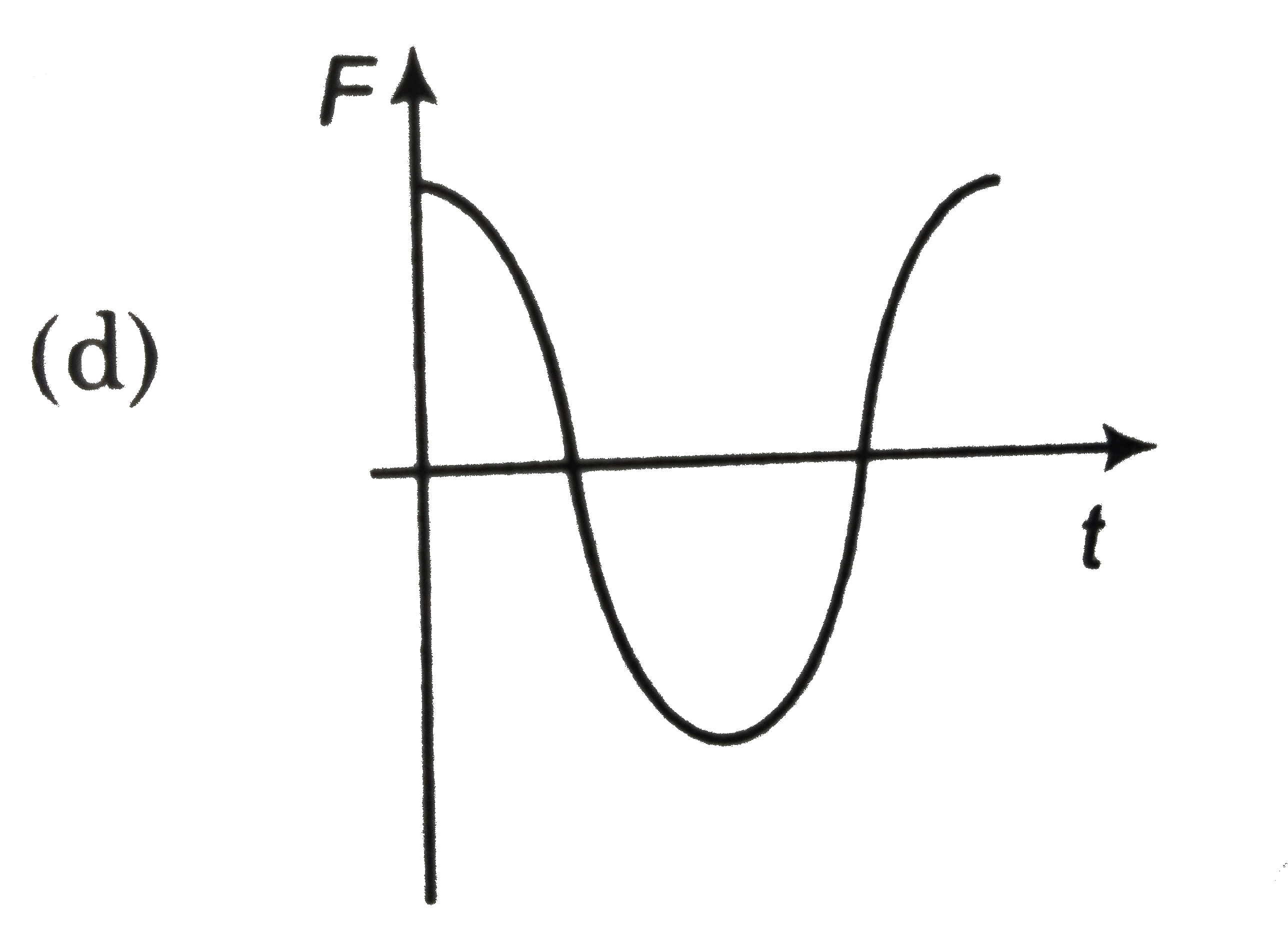
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
SIMPLE HARMONIC MOTION
DC PANDEY ENGLISH|Exercise Level 2 More Than One Correct|8 VideosSIMPLE HARMONIC MOTION
DC PANDEY ENGLISH|Exercise Level 2 Comprehension|2 VideosSIMPLE HARMONIC MOTION
DC PANDEY ENGLISH|Exercise Level 1 Subjective|39 VideosSEMICONDUCTORS AND ELECTRONIC DEVICES
DC PANDEY ENGLISH|Exercise More than One Option is Correct|3 VideosSOLVD PAPERS 2017 NEET, AIIMS & JIPMER
DC PANDEY ENGLISH|Exercise Solved paper 2018(JIPMER)|38 Videos
DC PANDEY ENGLISH-SIMPLE HARMONIC MOTION-Level 2 Single Correct
- A particle oscillates simple harmonic motion with a period of 16 s. Tw...
Text Solution
|
- A seconds pendulum is suspended from the ceiling of a trolley moving h...
Text Solution
|
- A particle is performing a linear simple harmonic motion. If the insta...
Text Solution
|
- In a vertical U - tube a column of mercury oscillates simple harmonica...
Text Solution
|
- A solid cube of side a and density rho(0) floats on the surface of a l...
Text Solution
|
- A uniform stick of length l is mounted so as to rotate about a horizon...
Text Solution
|
- Three arrangements of spring - mass system are shown in figures (A), (...
Text Solution
|
- Three arrangements are shown in figure. (a) A spring of mass m an...
Text Solution
|
- A block of mass M is kept on a smooth surface and touches the two spri...
Text Solution
|
- A particle moving on x - axis has potential energy U = 2 - 20x + 5x^(2...
Text Solution
|
- A block of mass m, when attached to a uniform ideal apring with force ...
Text Solution
|
- A body performs simple harmonic oscillations along the straight line A...
Text Solution
|
- In the given figure, two elastic rods P and Q are rigidly joined to en...
Text Solution
|
- A particle executes SHM of period 1.2 s and amplitude 8cm. Find the ti...
Text Solution
|
- A wire frame in the shape of an equilateral triangle is hinged at one ...
Text Solution
|
- A particle moves along the x - axis according to x = A[1 + sin omega t...
Text Solution
|
- A small bob attached to a light inextensible thread of length l has a ...
Text Solution
|
- A stone is swinging in a horizontal circle of diameter 0.8m at 30 rev/...
Text Solution
|
- Part of SHM is graphed in the figure. Here, y is displacement from mea...
Text Solution
|
- A particle performs SHM with a period T and amplitude a. The mean velo...
Text Solution
|