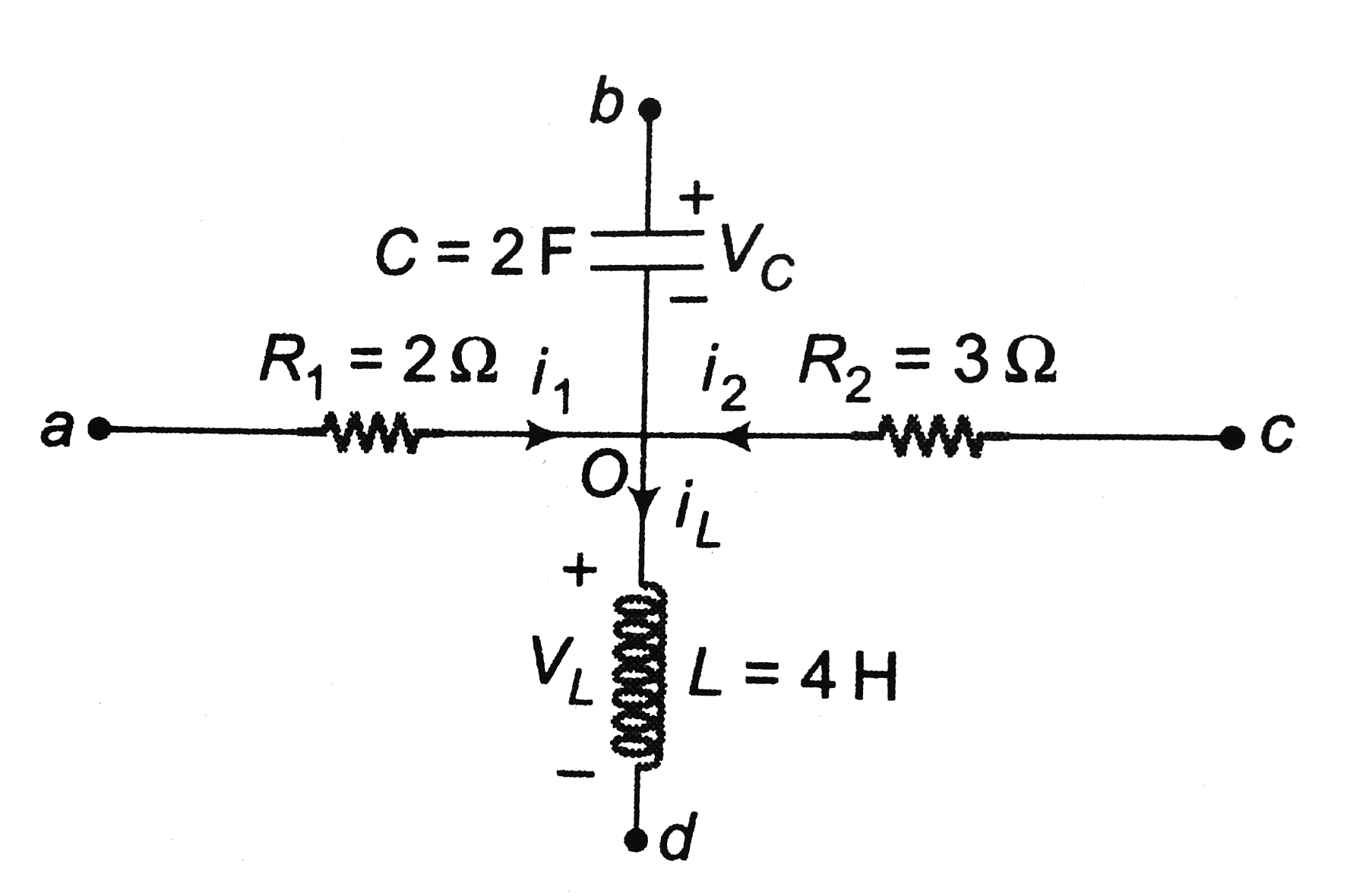a. Charge stored in the capacitor at time t,
` q=CV_C`
`= (2)(3e^(-2t))`
`= 6e^(-2t)C`
`:. i_c=(dq)/(dt)=12e^(-2t)A`
(Direction of current is form `b` to `O`)
Applying junction rule at `O`,
`i_L=i_1+i_2+i_e=10e^(-2t)+4-12e^(-2t)`
`=(4-2e^(-2t))A`
`[2+2(1-e^(-2t))]A`
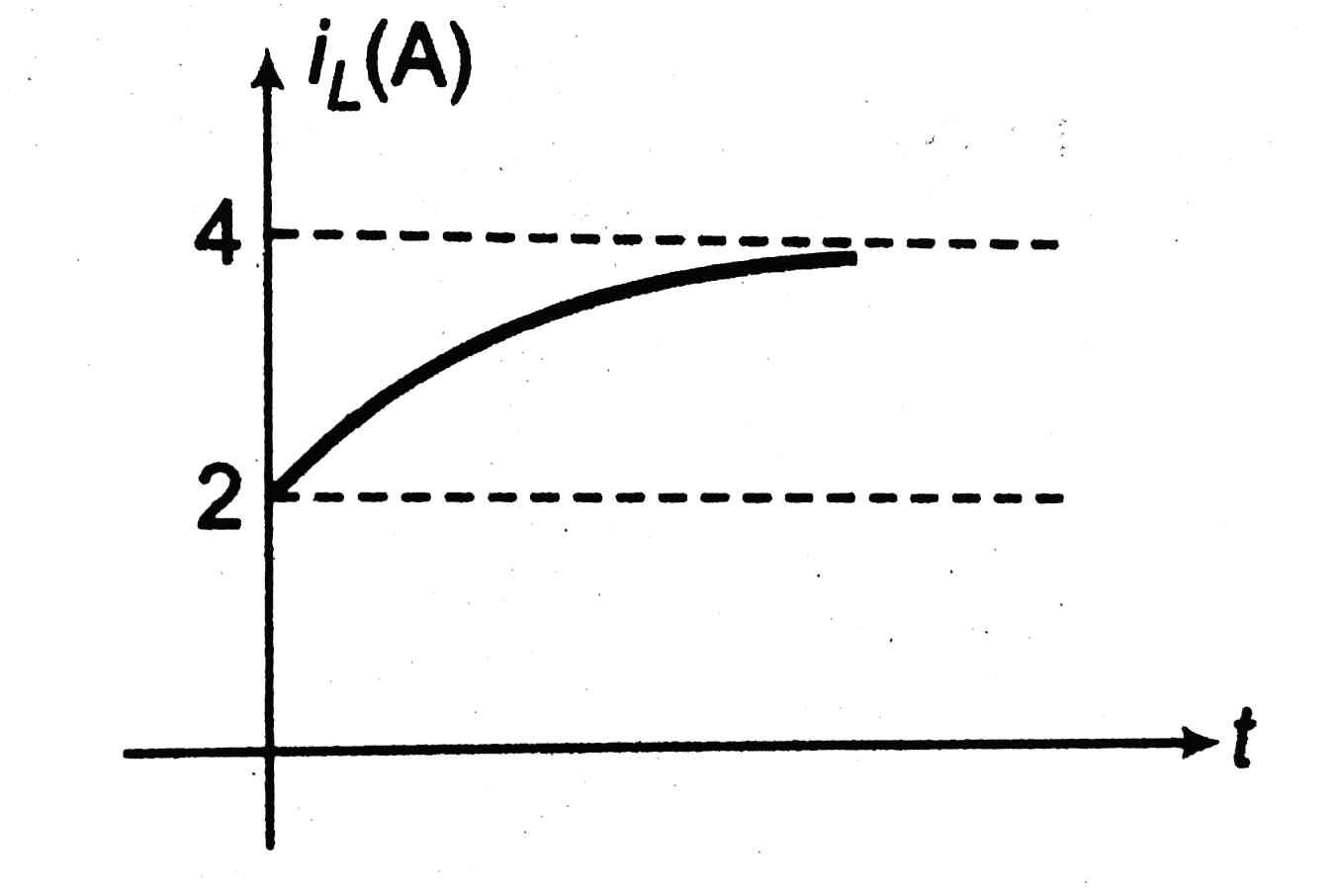
`i_L` versus time graph is as show in figure.
`i_L` increases from `2A` to `4A` exponentially .
`V_L=V_(Od)=L(di_L)/(dt) =(4) d/(dt)(4-2^(-2t))`
`=16 e^(-2t)V`
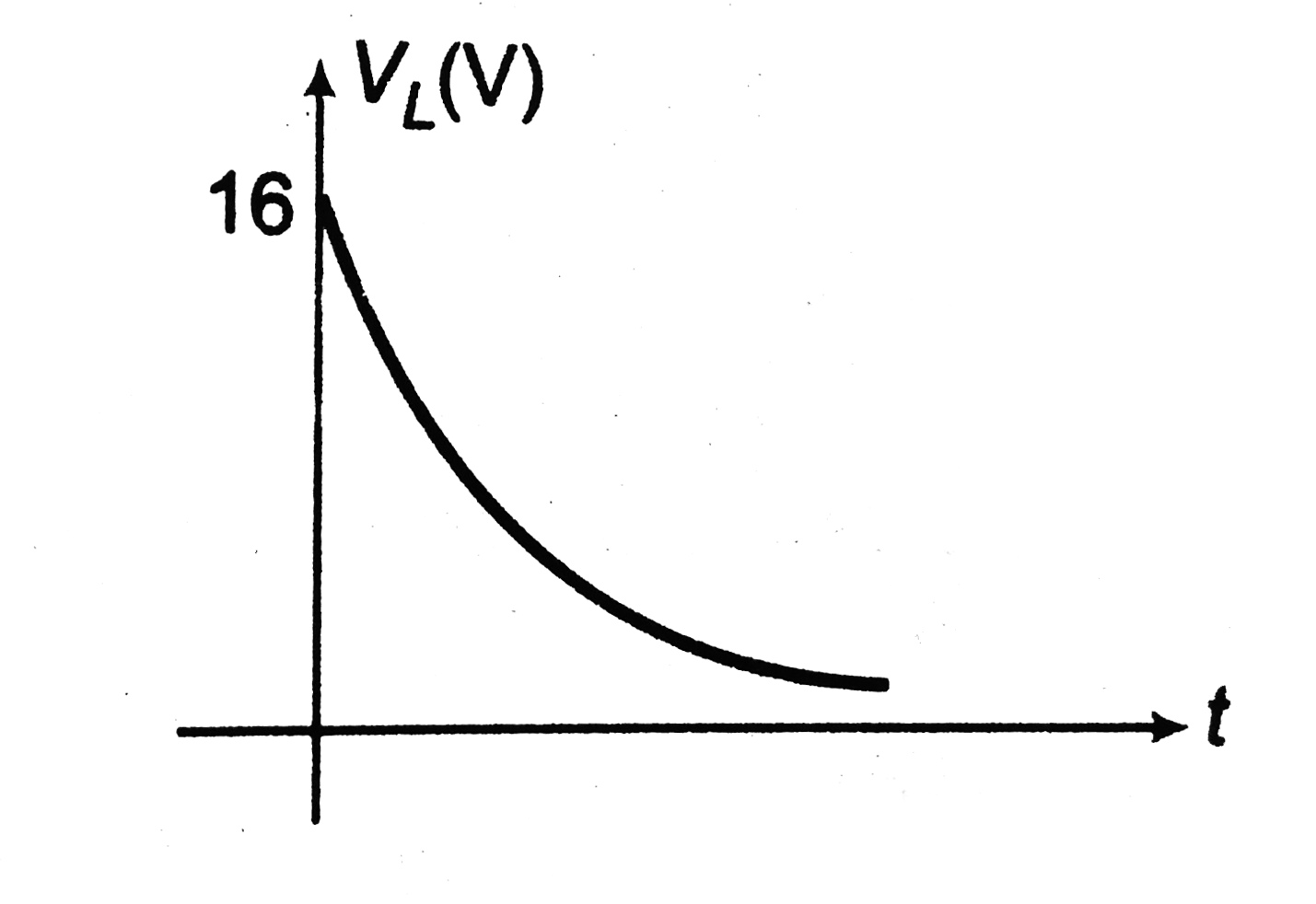
`V_L` versus time graph is an shown in figure.
`V_L` decreases exponentially from `16V` to `0`.
b. `V_(ac)=V_a-V_c`
`V_a-i_1R_1+i_2R_2=V_c`
`:. V_a-V_c=V_(ac)=i_1R1_1-i_2R_2`
substituting the values we have
`V_(ac)=(10e^(-2t))(2)-(4)(3)`
`V_(ac)=(20e^(-2t)-12)V`
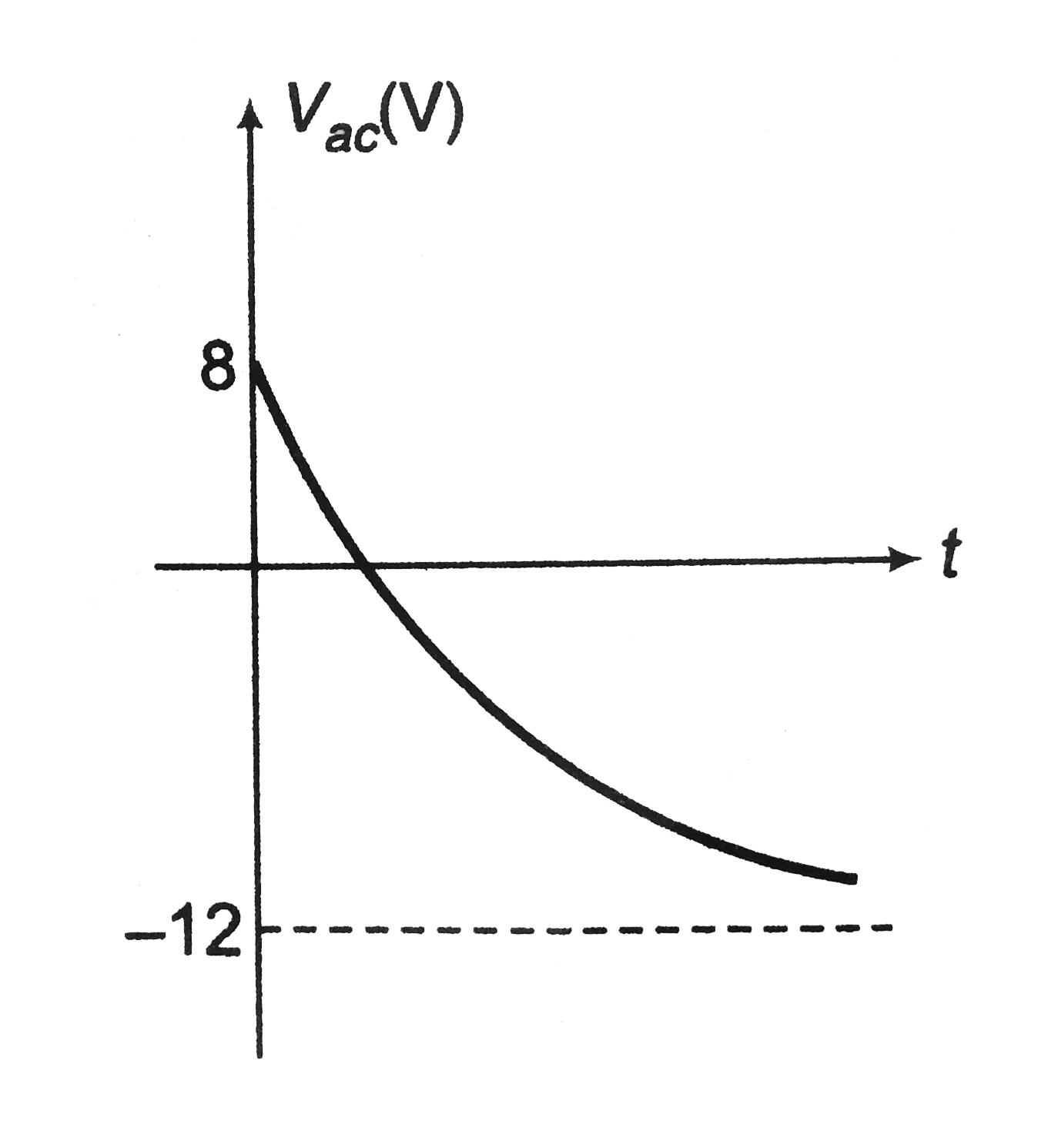
At `t=0, V_(ac)=8V` and at `t=oo, V_(ac)=-12V`
Therefore `V_(ac)` decreases exponentially from 8 to `-12V`.
`V_(ab)=V_a-V_b`
`V_a-i_1R_1+V_C=V_b`
`:. V_a-V_b=V_(ab)=i_1R_1-V_C`
Substituting the values , we have
`V_(ab)=(10e^(-2t))(2)=3e^(-2t)`
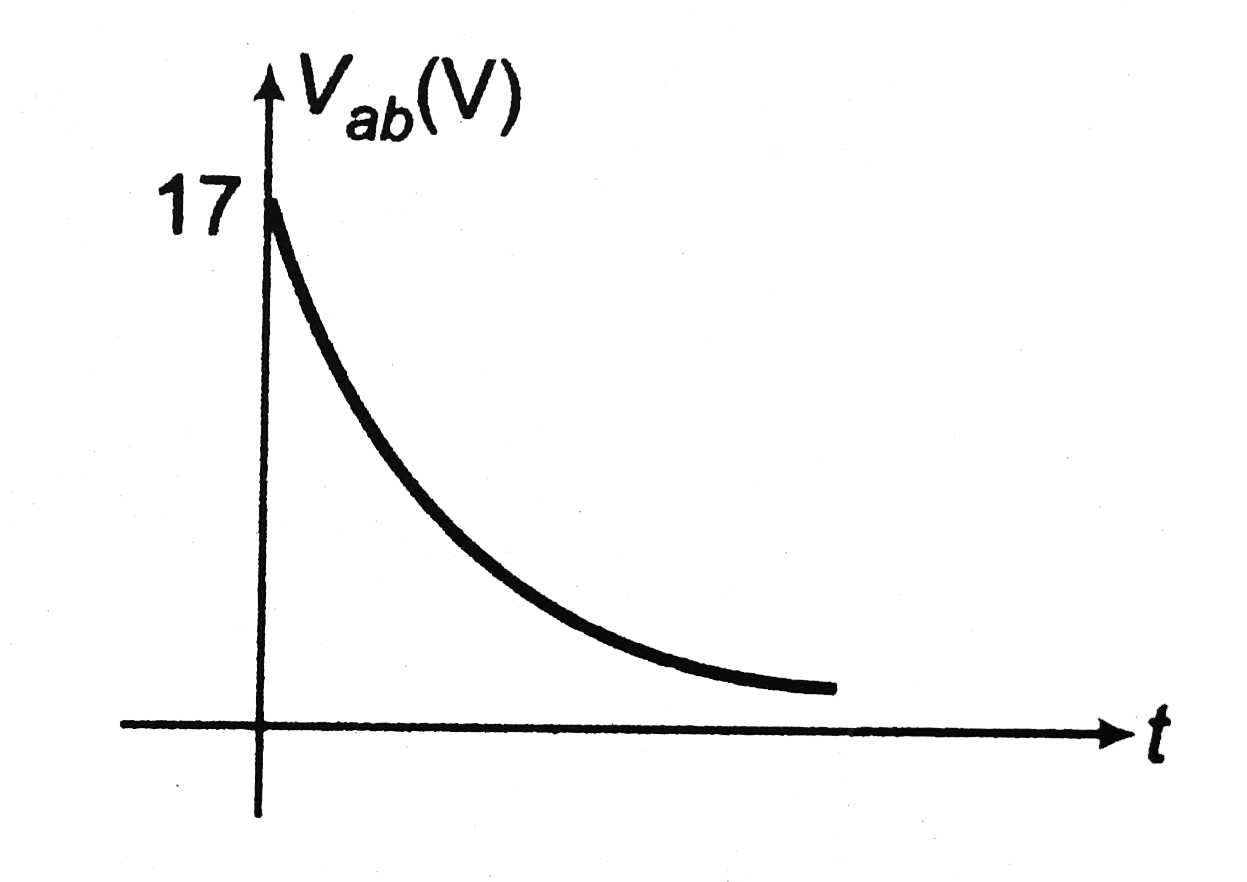
or `V_(ab)=17e^(-2t)V`
Thus `V_(ab)` decreses exponentially from `17 V` to `0`.
`V_(ab)` versus `t` graph is shown in figure.
`V_(cd)=V_C-V_d`
`V_d-i_2R_2-V_L=V_4`
`:. V_c-V_d=V_(cd)=i_2R_2+V_L`
Substituting the values we have
`V_(cd)=(4)(3)+16e^(-2t)`
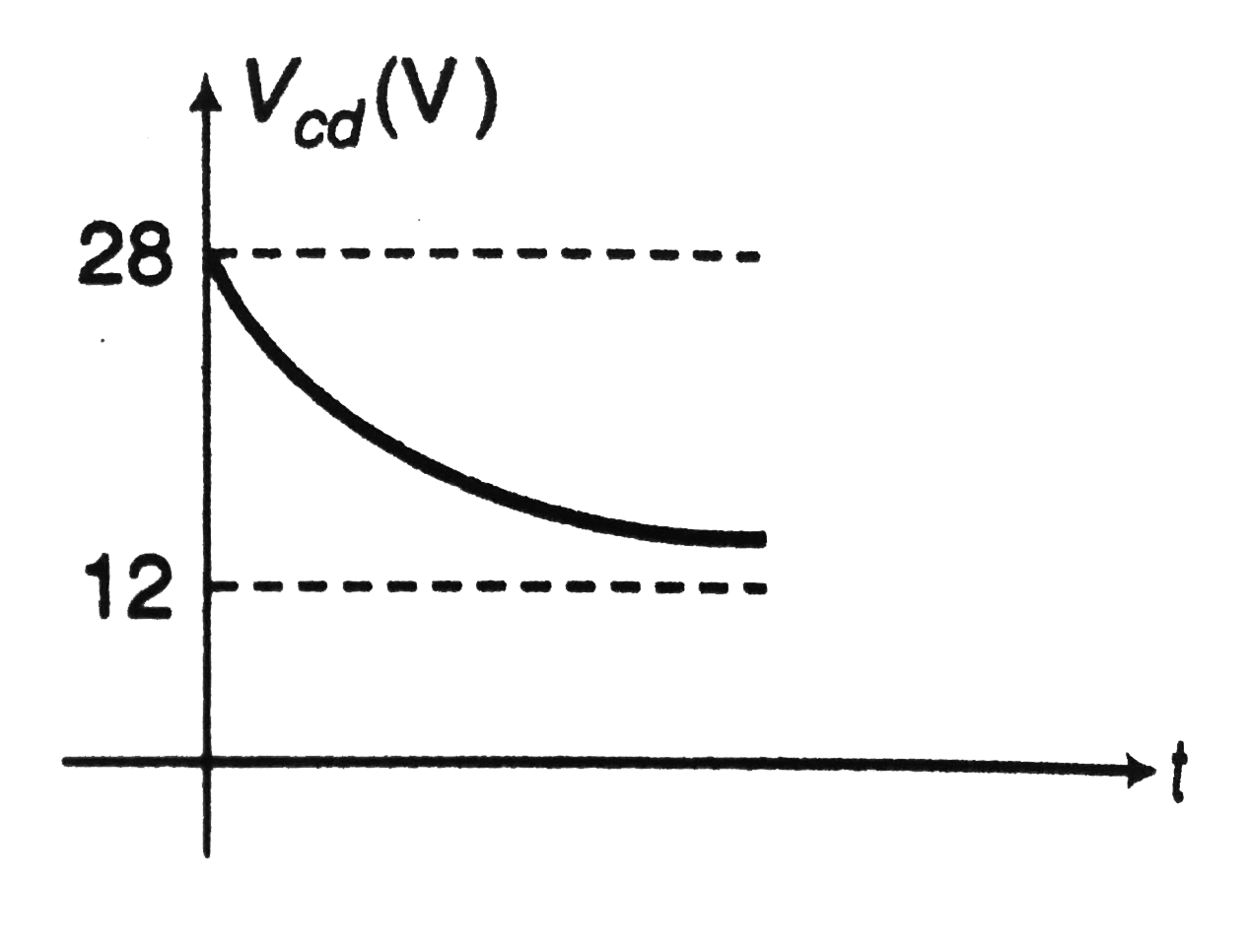
`V_(cv)=(12+16e^(-2t))V`
At `t=0, V_(cd)=28` and at `t=oo, V_(cd)=12V`
i.e. `V_(cd)` decreases exponentially from `28 V` to `12 V`
`V_(cd)` versus t graph is shown in figure.