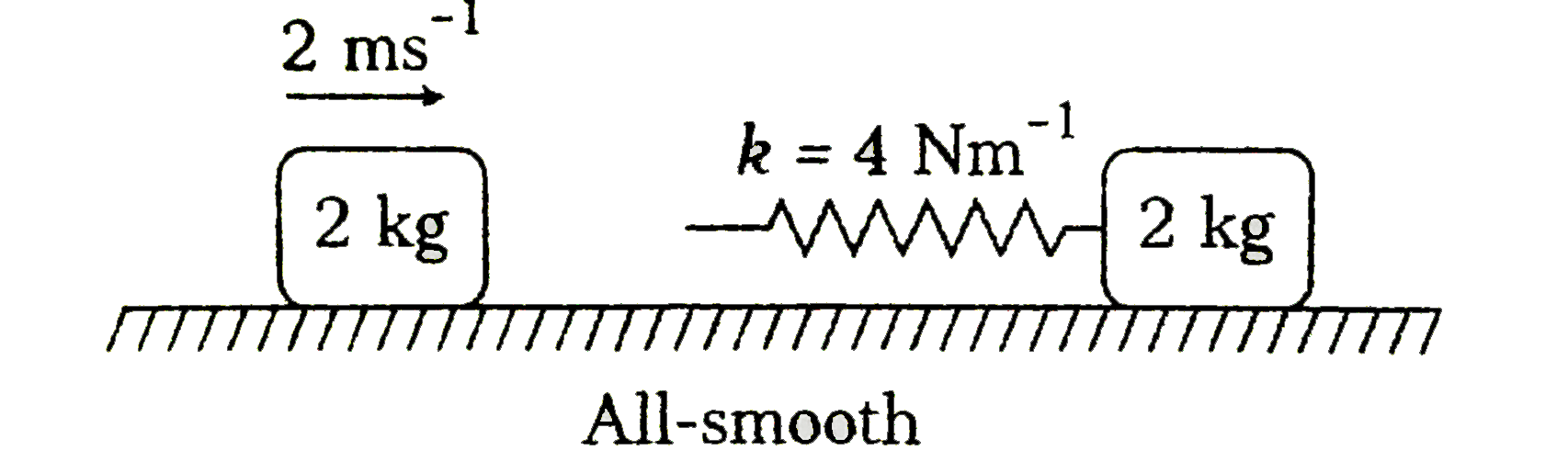Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
CENTRE OF MASS
DC PANDEY ENGLISH|Exercise Medical entrances gallery|27 VideosCENTRE OF MASS
DC PANDEY ENGLISH|Exercise Assertion and reason|21 VideosCALORIMETRY AND HEAT TRANSFER
DC PANDEY ENGLISH|Exercise Medical entrance s gallery|38 VideosCENTRE OF MASS, IMPULSE AND MOMENTUM
DC PANDEY ENGLISH|Exercise Comprehension type questions|15 Videos
Similar Questions
Explore conceptually related problems
DC PANDEY ENGLISH-CENTRE OF MASS-Match the coloumns
- If net force on a system of particles is zero. Then {:(,"Column I",,...
Text Solution
|
- Four point masses are placede at four corners of a square of side 4m a...
Text Solution
|
- In the diagram shown in figure mass of both the balls in same. Match t...
Text Solution
|
- A particle of mass 1 kg has velocity vec(v)(1) = (2t)hat(i) and anothe...
Text Solution
|
- In the arrangement shown in figure match the following {:("column...
Text Solution
|
- A particle of mass m, kinetic energy K and momentum p collides head on...
Text Solution
|
- A particle of mass 1 kg is projected upwards with velocity 60ms^(-1). ...
Text Solution
|
- Match the following: (P = momentum of particle, K = kinetic energy of ...
Text Solution
|
- In a two block system in figure match the following. {:("Column1","...
Text Solution
|