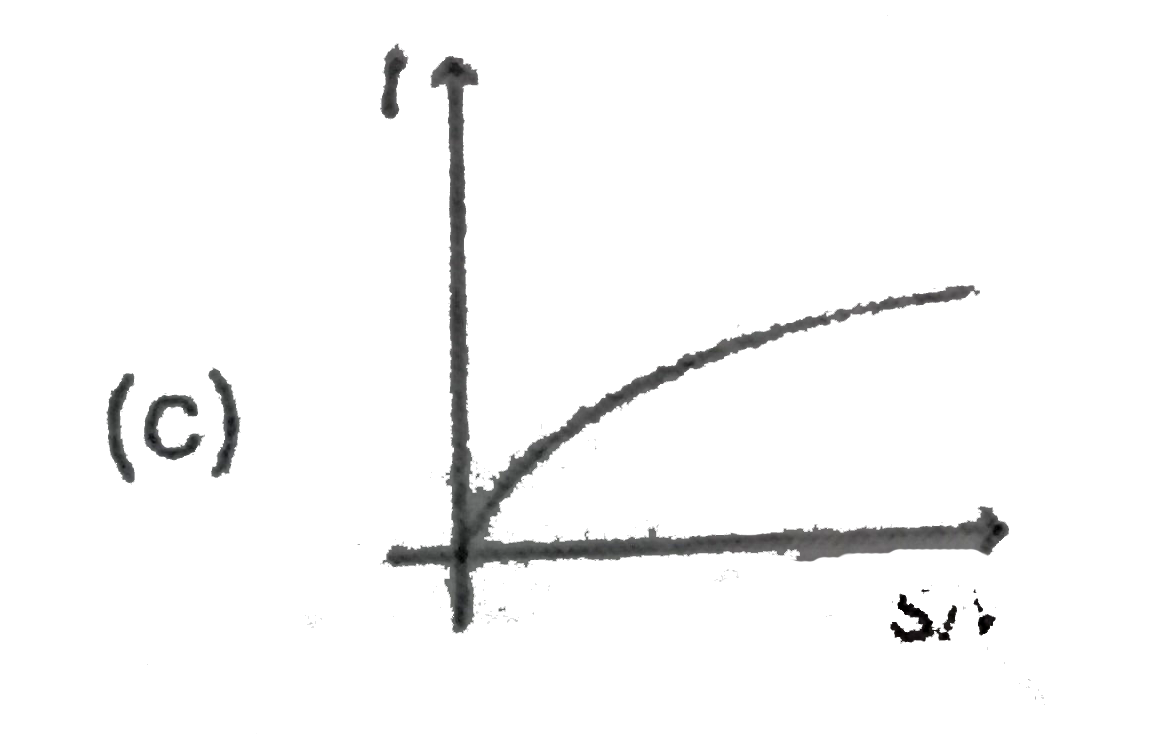
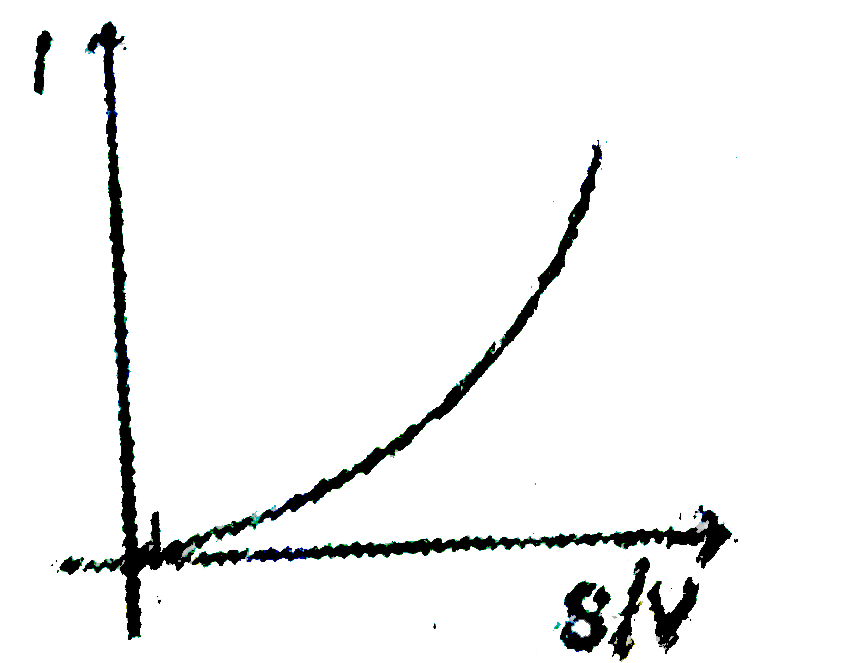
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
WORK, POWER AND ENERGY
DC PANDEY ENGLISH|Exercise B More than One Option is Correct|26 VideosWORK, POWER AND ENERGY
DC PANDEY ENGLISH|Exercise C Comprehension Type Questions|18 VideosWORK, POWER AND ENERGY
DC PANDEY ENGLISH|Exercise E Integer Type Questions|11 VideosWORK, ENERGY AND POWER
DC PANDEY ENGLISH|Exercise MEDICAL ENTRACES GALLERY|33 Videos
Similar Questions
Explore conceptually related problems
DC PANDEY ENGLISH-WORK, POWER AND ENERGY-A Only One Option is Correct
- A body is displaced from (0,0) to (1 m, 1m) along the path x = y by a ...
Text Solution
|
- A self-propelled vehicle of mass m, whose engine delivers a constant p...
Text Solution
|
- A body is moved from rest along a straight line by a machine deliverin...
Text Solution
|
- A forceF = (2hat(i)+5hat(j)+hat(k))N is acting on a particle. The part...
Text Solution
|
- A vertical spring of force cosntant 100 N//m is attached with a hangin...
Text Solution
|
- A partical is realeased from the top of two inclined rought surface of...
Text Solution
|
- System shown in figure is released from rest . Pulley and spring is ma...
Text Solution
|
- Force acting on a particale is (2hat(i)+3hat(j))N. Work done by this f...
Text Solution
|
- An object of mass m slides down a hill of arbitrary shape and after tr...
Text Solution
|
- A block of mass m slides down a rough inclined plane of inclination th...
Text Solution
|
- A 1.5-kg block is initially at rest on a horizontal frictionless surfa...
Text Solution
|
- In the above problem, the maximum positive displacement x is
Text Solution
|
- A block of mass 1 kg is attached to one end of a spring of force const...
Text Solution
|
- Two block of masses m(1) and m(2) connected by a light spring rest on ...
Text Solution
|
- A block of mass m is attached with a massless spring of force constant...
Text Solution
|
- The potential energy of a particle of mass m is given by U=(1)/(2)kx^(...
Text Solution
|
- A body of mass 2 kg is moved from a point A to a point B by an externa...
Text Solution
|
- A block of mass m = 0.1 kg is released from a height of 4m on a curved...
Text Solution
|
- A system consists of two cubes of mass m(1), and m(2) respectively con...
Text Solution
|
- A block mass m = 2 kg is moving with velocityv(0) towards a mass less ...
Text Solution
|