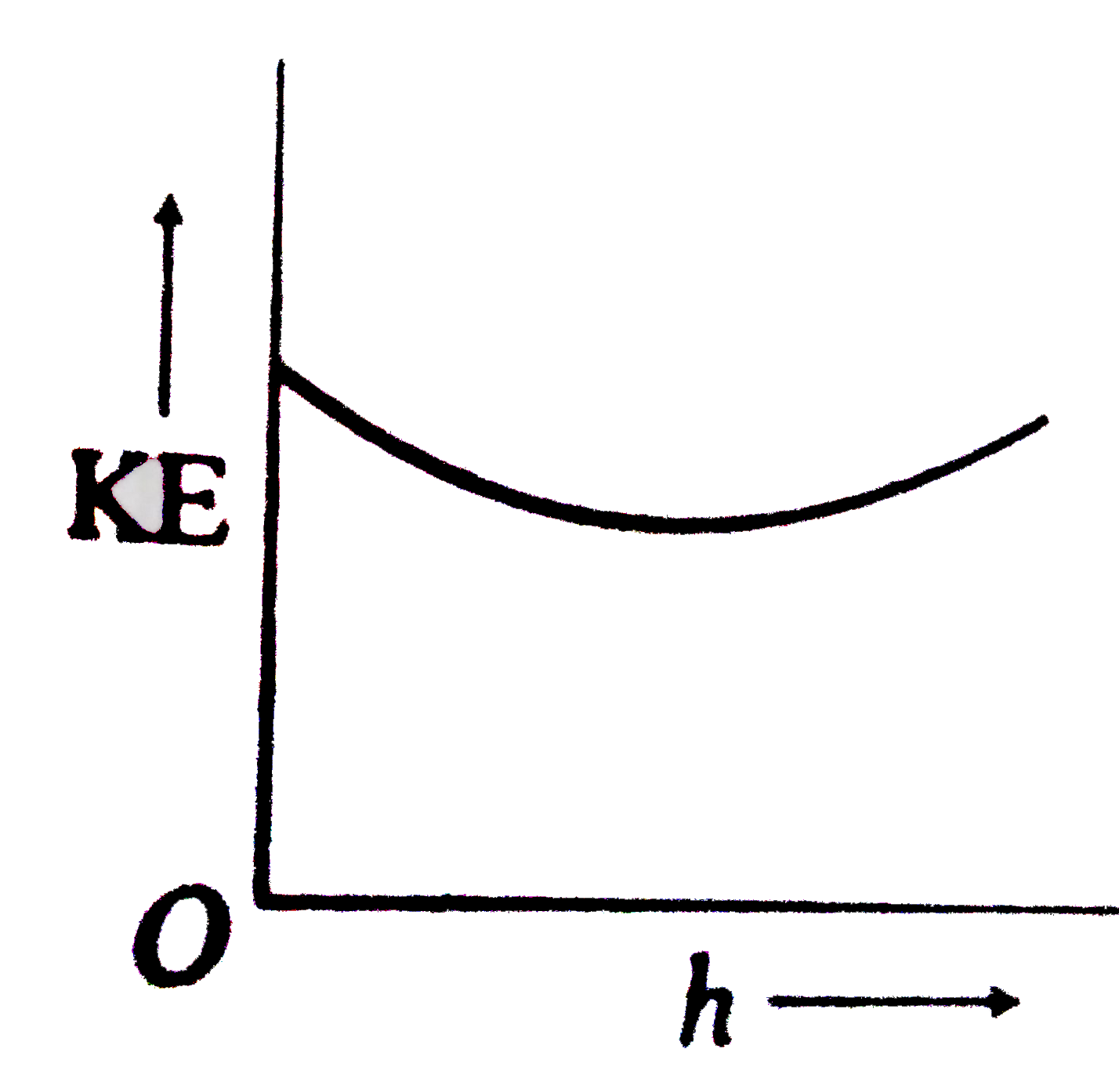
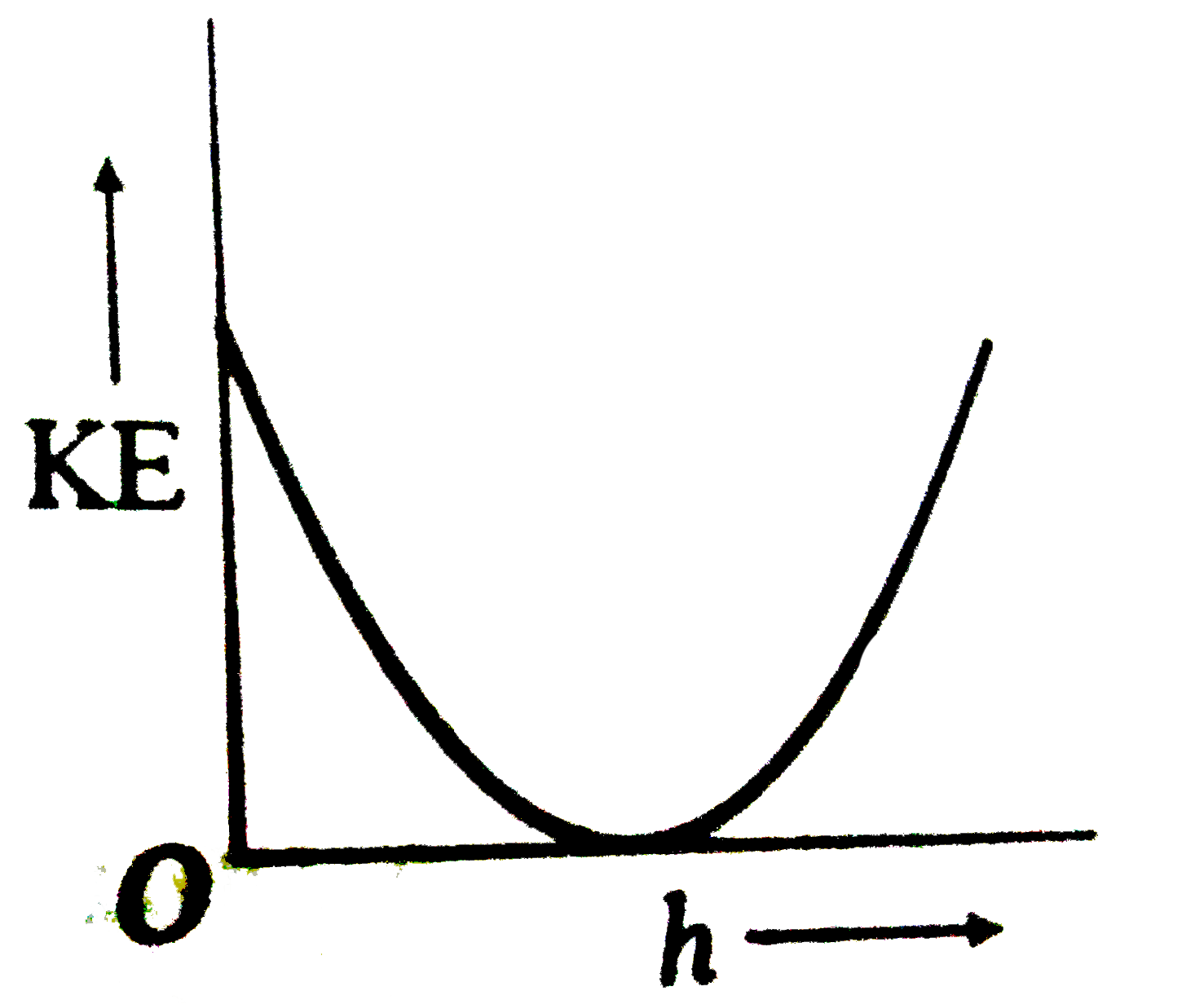
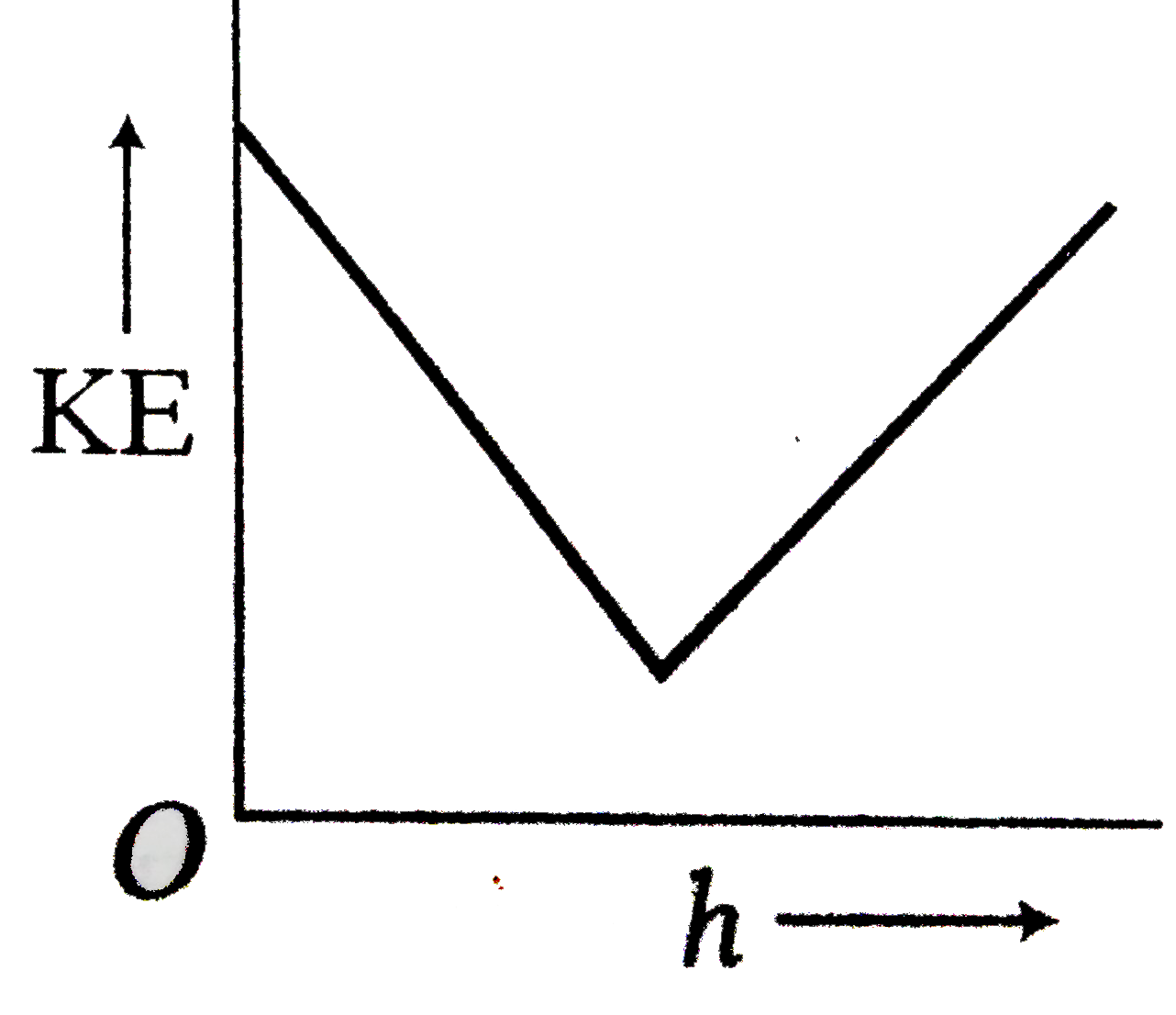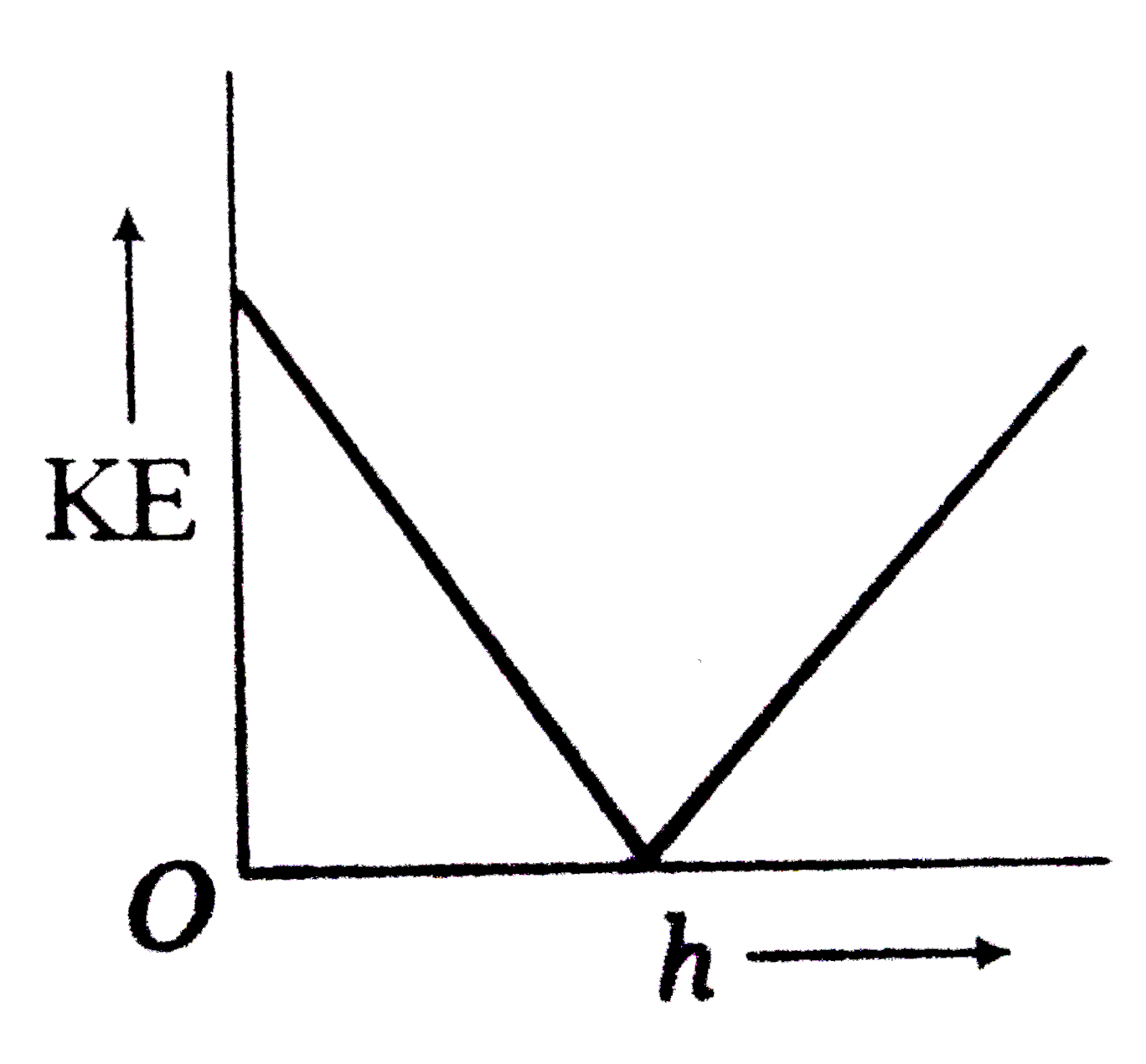A ball is thrown up with a certain velocity at angle `theta` to the horizontal. The kinetic energy varies with height h of the particle as:

Options

A.
B.
C.
D.

Explanation

To solve the problem of how the kinetic energy of a ball thrown at an angle `theta` to the horizontal varies with height `h`, we can follow these steps:

### Step 1: Understand the Initial Conditions
- A ball is thrown with an initial velocity \( v_0 \) at an angle \( \theta \) to the horizontal.
- The initial kinetic energy (KE) at the point of release (point O) is given by:
\[ KE_O = \frac{1}{2} m v_0^2 \]
- The potential energy (PE) at point O can be considered zero since we can take this point as our reference level.

### Step 2: Apply Conservation of Energy
- According to the conservation of mechanical energy, the total mechanical energy at the initial point (O) is equal to the total mechanical energy at any point (A) at height \( h \):
\[ KE_O + PE_O = KE_A + PE_A \]
- Since \( PE_O = 0 \), we have:
\[ \frac{1}{2} m v_0^2 = KE_A + mgh \]

### Step 3: Express Kinetic Energy at Height \( h \)
- Rearranging the equation gives us the kinetic energy at height \( h \):
\[ KE_A = \frac{1}{2} m v_0^2 - mgh \]

### Step 4: Simplify the Expression
- Factoring out \( m \):
\[ KE_A = m \left( \frac{1}{2} v_0^2 - gh \right) \]
- This shows that the kinetic energy decreases linearly with increasing height \( h \).

### Step 5: Analyze the Graph
- The kinetic energy is maximum at the ground (when \( h = 0 \)) and decreases as the height increases.
- At the maximum height \( h_{max} \), the kinetic energy will not be zero because the ball still has horizontal velocity \( v_0 \cos \theta \). Thus, the kinetic energy at the highest point can be calculated as:
\[ KE_{max} = \frac{1}{2} m (v_0 \cos \theta)^2 \]
- The graph of kinetic energy (KE) versus height (h) will be a straight line with a negative slope, indicating that as height increases, kinetic energy decreases.

### Final Graph Representation
- The graph starts from \( KE = \frac{1}{2} m v_0^2 \) at \( h = 0 \) and decreases linearly, approaching a value that corresponds to the kinetic energy at the maximum height.

### Summary
- The kinetic energy of the ball decreases linearly with height \( h \) until it reaches its maximum height, where it retains some kinetic energy due to horizontal motion.