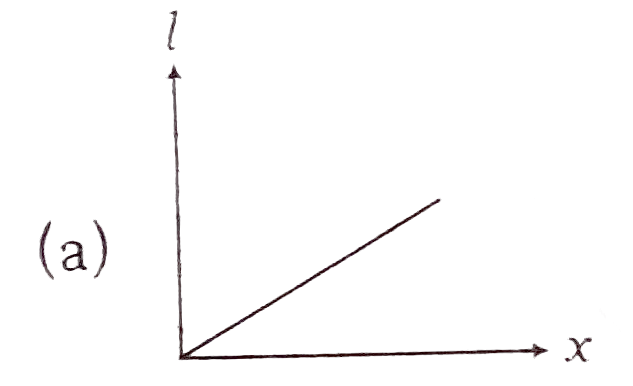
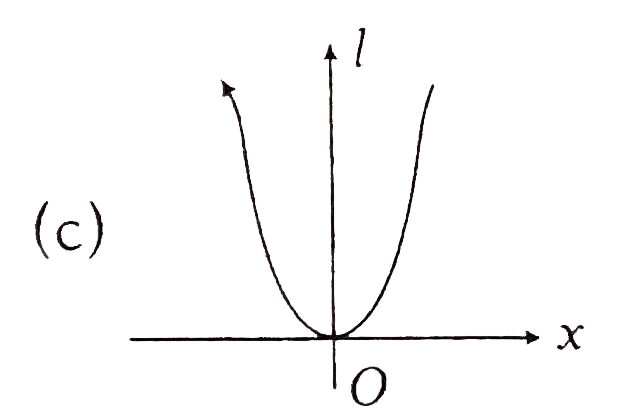
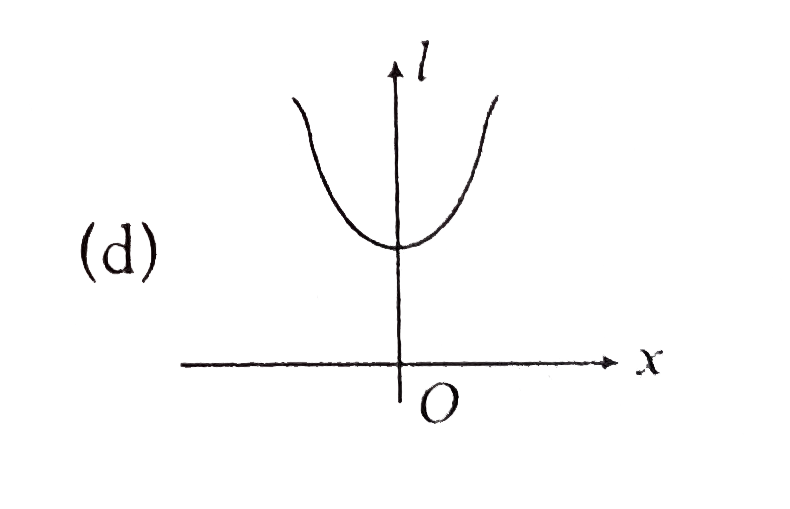
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
ROTATION
DC PANDEY ENGLISH|Exercise (B) Chapter Exercises|25 VideosROTATION
DC PANDEY ENGLISH|Exercise (C) Chapter Exercises|39 VideosROTATION
DC PANDEY ENGLISH|Exercise Check point 9.3|15 VideosRAY OPTICS
DC PANDEY ENGLISH|Exercise Integer type q.|14 VideosROTATIONAL MECHANICS
DC PANDEY ENGLISH|Exercise Subjective Questions|2 Videos
Similar Questions
Explore conceptually related problems
DC PANDEY ENGLISH-ROTATION-(A) Chapter Exercises
- The moment of inertia of a cube of mass m and side a about one of its ...
Text Solution
|
- Two uniform, thin identical rods each of mass M and length l are joine...
Text Solution
|
- Figure represents the moment of inertia of the solid sphere about an a...
Text Solution
|
- A heavy particle is projected with a velocity at an angle with the hor...
Text Solution
|
- If a sphere of mass m moving with velocity u collides with another ide...
Text Solution
|
- A uniform rod of mass 2 kg and length 1 m lies on a smooth horizontal ...
Text Solution
|
- A particle 'P' is moving in a circle of radius 'a' with a uniform spee...
Text Solution
|
- A uniform round object of mass M, radius R and moment of inertia about...
Text Solution
|
- A wheel comprises a ring of radius R and mass M and three spokes of ma...
Text Solution
|
- A square is made by joining four rods each of mass M and length L. Its...
Text Solution
|
- A solid homogeneous sphere is moving on a rough horizontal surface, pa...
Text Solution
|
- A sphere cannot roll on
Text Solution
|
- A thin bar of mass m and length l is free to rotate about a fixed hori...
Text Solution
|
- A disc is free to rotate about a smooth horizontal axis passing throug...
Text Solution
|
- <img src="https://d10lpgp6xz60nq.cloudfront.net/physicsimages/BMSDPP01...
Text Solution
|
- Two identical satellites are moving around the Earth in circular orbit...
Text Solution
|
- A solid sphere of mass 2 kg rolls up a 30^(@) incline with an initial ...
Text Solution
|
- The figure shows a uniform rod lying along the X-axis. The locus of al...
Text Solution
|
- A cord is wound around the circumference of wheel of radius r. The axi...
Text Solution
|
- A solid sphere rolls without slipping and presses a spring of spring c...
Text Solution
|