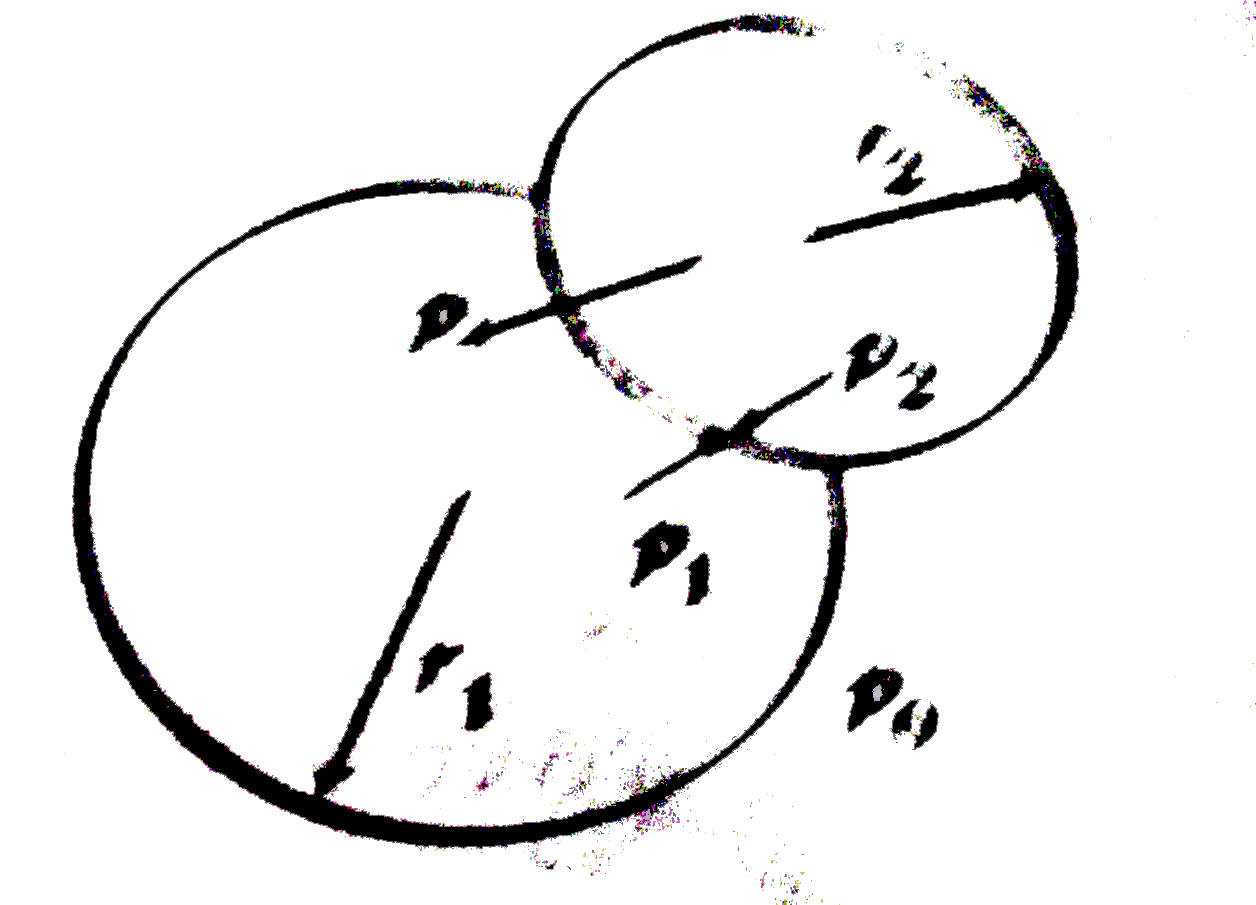Text Solution
Verified by Experts
Topper's Solved these Questions
FLUID MECHANICS
DC PANDEY ENGLISH|Exercise Example 13.33|1 VideosFLUID MECHANICS
DC PANDEY ENGLISH|Exercise Example 13.34|1 VideosFLUID MECHANICS
DC PANDEY ENGLISH|Exercise Example 13.31|1 VideosEXPERIMENTS
DC PANDEY ENGLISH|Exercise Subjective|15 VideosGENERAL PHYSICS
DC PANDEY ENGLISH|Exercise INTEGER_TYPE|2 Videos
Similar Questions
Explore conceptually related problems