Text Solution
Verified by Experts
Topper's Solved these Questions
SUPPLEMENTARY EXAM QUESTION PAPER JULY - 2014
SUNSTAR PUBLICATION|Exercise PART-D (V. Answer any two of the following.) |3 VideosP.U. BOARD LATEST MODEL QUESTION PAPER-3
SUNSTAR PUBLICATION|Exercise PART-D|11 VideosSUPPLEMENTARY EXAM QUESTION PAPER JULY -2015
SUNSTAR PUBLICATION|Exercise PART-D|11 Videos
Similar Questions
Explore conceptually related problems
SUNSTAR PUBLICATION-SUPPLEMENTARY EXAM QUESTION PAPER JULY - 2014-PART-D (VI. Answer any three of the following questions.)
- Two charges 3x10^(-8)C & -2x10^(-8)C are located 15 cm apart. At what ...
Text Solution
|
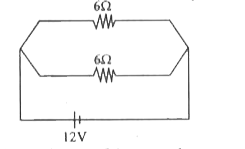
- A network of resistors is connected to a 12V battery as shown in fig. ...
Text Solution
|
- A pure inductor of 25mH is connnected to a source of 220V and 50 Hz. F...
Text Solution
|
- A prism of angle 60^(0) produces angle of minimum deviation of 40^(0)....
Text Solution
|
- The work function of caesium metal is 2.14 ev. When light of frequency...
Text Solution
|