Home
Class 12
MATHS
You are given the following data: ...

You are given the following data:

Correlation coefficient between x and y=0.66. Find the equations of the lines of regression.

Text Solution

Verified by Experts

The correct Answer is:
Regression equation of y or x : y = 0.48 x + 67.82
Regression equation of x or y : x = 0.91 y - 41. 35
Promotional Banner

Topper's Solved these Questions

  • MODEL TEST PAPER 20

    ICSE|Exercise SECTION B|10 Videos

  • MODEL TEST PAPER 15

    ICSE|Exercise SECTIONS-C|11 Videos

  • MODEL TEST PAPER-11

    ICSE|Exercise SECTION-C|9 Videos

Similar Questions

Explore conceptually related problems

If the regression coefficients be given b_(yx)=1.6 and b_(xy)=0.4 then find the sum of the slopes of the two regression lines.

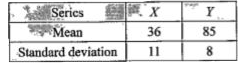
The following results were obtained with respect to two variable x and y: sumx = 30, sum y = 42, sumxy = 199, sumx^(2) = 184, sumy^(2) = 318, n=6 . Find the following: (i) The regression coefficients. (ii) Correlation coefficient between x and y. (iii) Regression equation of y on x. (iv) The likely value of y when x = 10.

From the following data, find () regression coefficients (ii) regression equations.

From the following data, find Regression equations.

Find the regression coefficient b_(yx) and b_(xy) when the lines of regression are 6x-5y+10=0, 10x-3y-28=0 .

If the two regression coefficients are - 0.4 and -1.6, then the coefficient of correlations is

There are two series of index numbers: P for price index and S to stock of a commodity. The mean and standard deviation of P are 100 and 8 and of S are 103 and 4 respectively. The correlation coefficient between the two series is 0.4. With these data, obtain the regression lines of P on S and S on P.

The coefficient of correlation between the values denoted by x and y is 0.5. The standard deviation of x is 5 and that of y is 4. Find the angle between the lnes of regression.

You are given the following data, obtain the regression equation and estimate the yield of crops when the rainfall is 29cm. Given that coefficient of correlation between yield and rainfall= 0.52