Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
ICSE-THE TRIANGLE AND ITS PROPERTIES-REVISIONS EXERCISE
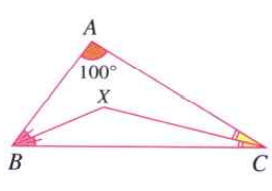
- In DeltaABC,angle=100^(@). Line segment BX divides angleB into two equ...
Text Solution
|
- In the given figure, name a median and an altitude. .
Text Solution
|
- A median and an altitude of an obtuse-angled triangle lie outside the ...
Text Solution
|
- Find the measure of the angles of a triangle which has one of its exte...
Text Solution
|
- Find the values of x and y in the given figure. .
Text Solution
|
- Find the three angles of a triangle that are in the ratio 2:3:4.
Text Solution
|
- Find the values of x and y in the given figure. .
Text Solution
|
- Find the values of x and y in the given figure.
Text Solution
|
- In DeltaABC, angleC=40^(@),BQ and AR are the angle bisectors of angleB...
Text Solution
|
- Find the value of angleA+angleB+angleC+angleD+angleE. .
Text Solution
|
- Given AB||CD, EF and GH are transversal to AB and CD. Find x.
Text Solution
|
- The sides of a triangle are 6 cm, 10 cm, and a cm. where a is a whole ...
Text Solution
|
- Find the third side of an isosceles triangle whose two sides are 9 cm ...
Text Solution
|
- In a right-angled triangle, the square of the longest side is 625 sq. ...
Text Solution
|
- Two poles of height 13 feet and 25 feet are standing at two ends of a ...
Text Solution
|
- Find the length AB using Phythagoras' theorem.
Text Solution
|